交易|交易持仓出现亏损，如何才能心甘情愿的严格止损？交易

文章图片

上一篇文文章《为何我们通常“不愿止损”》提出：
综合分析，交易中当出现浮亏时，我们很可能选择B“抗单” ，原因如下：
第一，根据前景理论，面对损失时，我们是风险喜好者，所以当出现浮亏时，我们倾向于冒险，选择“抗单” ，以希望能扛回来，不亏钱；
第二，根据概率优势，当出现浮亏时，如果不止损， 80%的概率能够扛回来，即大概率上，我们是不会亏钱，所以站在大概率的角度上，我们选择“不止损”；
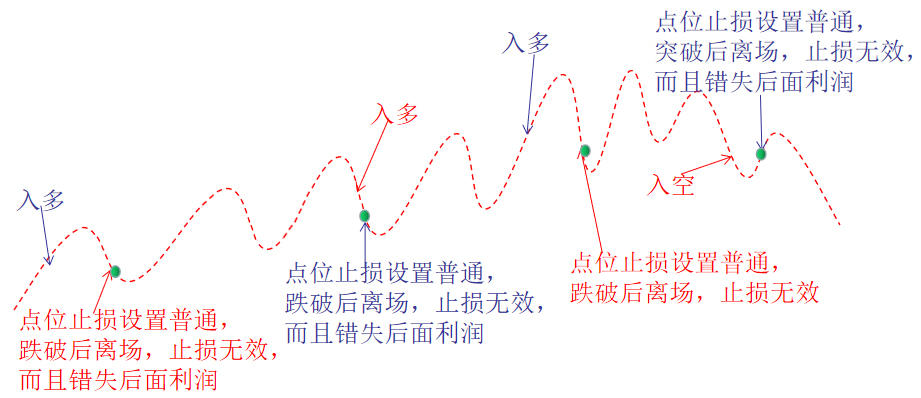
第三，事后来看，大部分情况下，如果当时不止损，浮亏是可以扛回来的，止损是无效的，至少看起来“止损是错误”的，加深了不止损的信念；
第四，选择A“止损” ，结局很可能是“S” ，虽然是慢S 。每刀不致命，但刀刀割肉，割的头破血流、皮毛不存，也是S ，而且这种痛苦的持续时间还很长，还不如一刀致命，选择“抗单”带来的猝S ，让人痛苦的时间短一些。所以既然都是S ，为何要选择“止损”呢？
四、前景理论的实验缺点：只有一次选择机会美国普林斯顿大学心理学教授卡内曼和特沃斯基提出了 “前景理论”（prospect theory），在面对损失时，做的实验：
A选项：百分之一百会损失100万；
B选项：51%的概率损失200万， 49%的概率损失0 。
因为只有一次选择机会，选择B的结果只能是亏200万和0两个结果，不可能有102万的结果，所以这种期望值的意义很小。此时，因为只有一次选择机会，概率就失去了意义，一切变得不确定，但A是确定的， A肯定会亏掉100万， B还可能不亏损，而且概率并不低，此时就容易选择B 。
我们对实验进行修改，现在不再是1次选择机会，而是1万次的选择机会，选项如下：
A选项：百分之一百会损失100；
B选项：51%的概率损失200 ， 49%的概率损失0 。
你有1万次的选择机会，请问，此时你是选择A ，还是选择B？
选择A ，你每次必然损失100 ，那么1万次，你肯定能损失100万。
选择B的话， 1万次的选择机会，事件次数多，你不可能每次都能蒙对“损失0” ，必然也有许多次遇到“损失200” ，概率会接近理论值，即“损失0”的概率趋近49% ， “损失200”的概率趋近51% ，那么选择B的话，你损失的资金就是趋近102万，无限接近，就可以认为损失102万，此时你是没有任何侥幸心理的，至少不可能抱有“亏损0”的侥幸。
在面对1万次的选择机会时，此时面对亏损时，就不如直接选择A ，因为A的损失小，至少B选项不可能让我们抱有“亏损0”的侥幸。
五、如何克服“不易止损”的问题？根据上面的行为实验，一般来说，在盈利时，我们是风险厌恶者，有盈利时就及时落袋为安，但在亏损时，就变成风险偏好者，不想接受亏损的事实，总会想着赌一把，等着被解套，虽然多次侥幸可以解套，但必然会出现无法解套的那一刻，爆仓是必然发生的，所以我们必须是要止损的；但是止损的话，我们又会面临连续多次止损的慢S结局。该怎么办呢？
一，给自己许多次的选择机会，证明“不止损”必会百分之一百S亡根据上述“前景理论”的实验，在面对损失时，我们容易成为风险偏好者，赌一赌的侥幸心里容易占上风。不过这个实验的缺点是“只有一次选择机会” ，如果给1万次的选择机会，则结果就会趋近期望值，我们的选择就会不同，赌一赌的侥幸心里就会消失。