『黑洞』如果将宇宙中所有原子的原子核和电子都紧挨在一起排列,有多大?
文章图片
【『黑洞』如果将宇宙中所有原子的原子核和电子都紧挨在一起排列,有多大?】
文章图片

文章图片

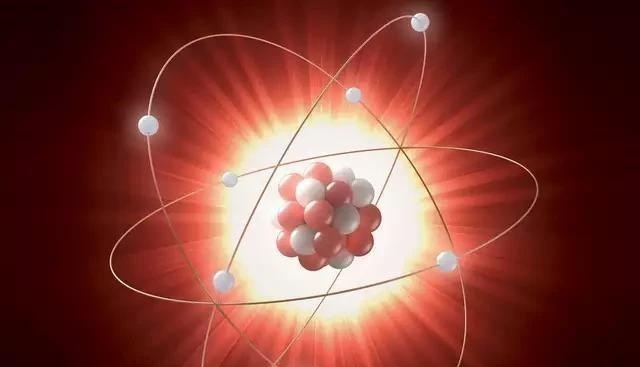
这是一个脑洞大开的问题 , 之所以产生这样的想法 , 来源于人们对原子及其内部结构了解地日益深入 。 我们在中学物理课上都学过 , 原子是由原子核以及核外电子所组成 , 其中原子核中又包含着质子和中子(H1是唯一没有中子的元素) , 虽然原子的体积非常微小 , 半径只有10^(-10)米级别 , 但是原子核的尺寸更小 , 其半径只有10^(-15)米级别 , 因此组成物质的原子 , 实际上中间是非常空旷的 , 超过99%的空间什么都没有 , 这也就给了人们以“压缩原子”的假想空间 。 按照这种假设 , 如果我们能够把宇宙中的所有物质中的原子都提取出来 , 并且将它们之间的空间全部压缩 , 一点空隙都不留 , 呈现出来的物体到底有多大呢?
当然 , 我们穷尽所有能力也不可能做出这样的实验 , 宇宙中也不可能给我们创造这样的条件去实现这样的结果 。 毕竟在微观世界领域 , 原子与原子之间有同性原子之间的库仑斥力作用 , 这种作用力连太阳内核1500万摄氏度、几百万个大气压条件下 , 也无法大几率地实现原子中质子与质子的结合 , 只能借助于量子隧穿效应 , 以很低的几率推动氢核聚变“温和”地发生 。
同时 , 电子在原子核外的排列 , 是以量子态的形式随机分布的 , 遵循同性相斥力和泡利不相容原理 。 所以 , 我们只能假设可以将原子核与电子紧紧相连在一起的情形发生 , 在此基础上做一些简单的分析和计算 。
如果纯粹地将原子核与电子进行罗列性地排列 , 那么只需要计算出宇宙中有多少个原子 , 然后估算出原子核和电子压缩之后所占的空间大小 。 计算宇宙中原子数量的方法有两种 , 第一是通过氢原子数进行估算 , 因为从太阳系来看 , 氢元素所占的比例大约在75%左右 , 而太阳的质量占据整个太阳系总质量的99.86% , 我们大致可以估算出可观测宇宙中的原子数量 , 即为可观测宇宙中的星系数量*每个星系平均的恒星数量*恒星的平均氢原子数量/75% , 据此可以估算出宇宙总原子数量为5*10^80个 。
第二种方法相对精确一些 , 方法主要是通过计算宇宙平均密度、普通物质的总量 , 在扣除暗物质和暗能量之后 , 再根据宇宙中最常见元素(氢、氦、氧)的丰度来计算原子的总数量 , 计算结果比较复杂 , 这里就不一一列出了 , 最后计算出的结果为7*10^79个 。 与上面一种方法相对比 , 差距并不是太大 , 这里我们取近似值10^80个来计算 。
如果将每个原子压缩成原子与电子紧密排列的情况 , 那么最后形成的物体体积的计算表达式为:10^80*4/3*π*(10^-10)^3*10^(-15) , 其中10^80是宇宙原子总数 , 4/3*π*(10^-10)^3为每个原子的体积 , 10^(-15)为压缩之后的原子体积与原始状态下原子的体积之比 。 我们最后计算得出的数值为:4.2*10^35立方米 , 相当于一个半径为4.6*10^11米的球体 。 如果以太阳为中心 , 那么这个球体的表面将延伸到4.6亿公里的区域 。
当然这只是一个理想状态 , 实际上如果有外力能将原子核与电子紧紧相连 , 所提供的这种外力作用完全有可能将电子压进原子核之内 , 从而与原子核中的质子结合形成中子 , 宇宙中的中子星就是大质量恒星在生命晚期 , 在爆发超新星爆发之后所残留的核心部分继续发生坍缩所形成的一种天体 , 其密度非常之高 , 每立方厘米可以达到上千亿吨 。 可观测宇宙中的所有原子和电子 , 如果都形成这样的中子星 , 按照其平均密度来计算 , 其最后组合形成的球体半径将达到上百亿公里 。
- 科学家■如果宇宙由奇点大爆炸而来,那么奇点又是如何来的?
- 【科学家】科学家公布首张宇宙全景高清图像,在宇宙之外又是什么呢?
- 科学家▲科学家发现宇宙的终极是熵,这意味着什么?未来世界将一片混乱!
- 天文在线|有些是直接坍缩的,证据来了!黑洞并非都由恒星坍缩产生
- 天文在线|宇宙会以什么样的方式结束?科学家给出了不同的预测
- 爱因斯坦■100年前,爱因斯坦曾大胆预言黑洞,还预言了中国,如今字字应验
- 黑洞使者|科学家:或可用大气矿尘寻找外星生命,“第二地球”判定标准来了
- 「鲸鱼」盾牌座UY已不是宇宙最大恒星,新晋宇宙最大恒星有100亿个太阳大
- 火星一号|如果全用完怎么办?,全球每天用掉100亿个二维码
- 辽沈晚报抚顺时刻|引力波观测到迄今最轻黑洞
