数学@只有清楚高考热点，才能战胜高考，收好这份复习建议数学

文章图片

文章图片

文章图片

文章图片

高考作为整个社会最重要的考试之一，一方面为高等院校选拔人才，促进社会科技的发展，另一方面也对中学教育提供指引和方向。高考既然作为人才选拔的考试，肯定不会只是考查考生知识掌握程度那么简单，还会重点考查考生分析问题和解决问题的能力。

像立体几何有关的试题，能很好的考查考生的空间想象能力，要想正确解决这些问题，常常需要考生具有一定的综合能力。
在每年的高考中，与立体几何有关的试题，如线线、线面、面面平行的性质和判定是考查的重点之一，线面平行又是平行的重要题型。处理线面平行问题要注意线线、线面、面面的相互转化，采用辅助线(面)是证线面平行的关键。
综观近几年高考数学试题，涉及“线面”的试题难度一般不大，基本题型和中等难度的综合题型仍会继续保留。不过，随着空间向量的出现，利用空间向量进行论证和计算的问题肯定会出现，但难度不会太大。
“线面”有关的高考数学试题分析，讲解1：
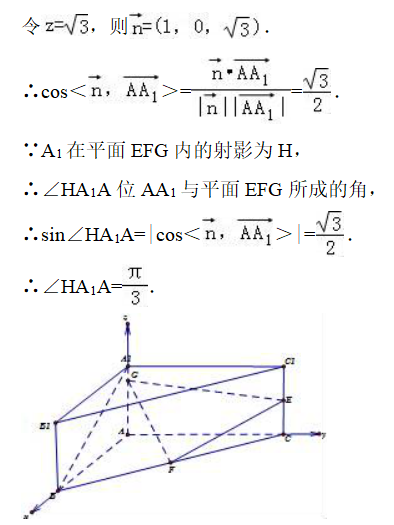
已知三棱柱ABC﹣A1B1C1中， A1A⊥底面ABC ， ∠BAC=90° ， A1A=1 ， AB=√3 ， AC=2 ， E、F分别为棱C1C、BC的中点．
（Ⅰ）求证AC⊥A1B；
（Ⅱ）求直线EF与A1B所成的角；
（Ⅲ）若G为线段A1A的中点， A1在平面EFG内的射影为H ，求∠HA1A．
考点分析：
直线与平面所成的角；棱柱的结构特征．
题干分析：
（I）由AC⊥AB ， AC⊥AA1即可得出AC⊥平面ABB1A1 ，于是AC⊥A1B；
（II）以A为原点建立坐标系，求出坐标，计算cos＜＞即可得出直线EF与A1B所成的角；
（III）求出向量和平面EFG的法向量，则sin∠HA1A．
考生要掌握好平面基本性质、空间两条直线、直线和平面、两个平面的位置关系（特别是平行和垂直关系）以及它们所成的角与距离的概念。
同时更要能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定，进行论证和解决有关问题。
“线面”有关的高考数学试题分析，讲解2：
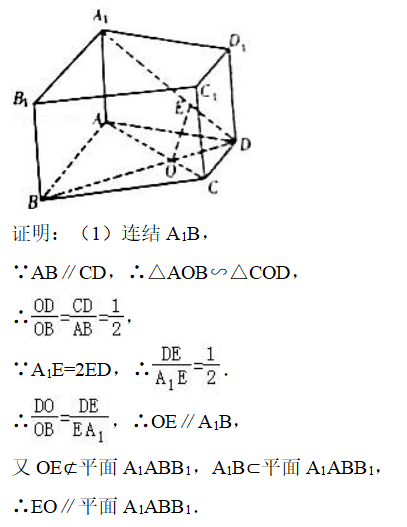
如图，在四棱柱ABCD﹣A1B1C1D1中， AB∥CD ， AB⊥AD ， AB=4 ， AD=2√2 ， CD=2 ， AA1=2 ，侧棱AA1⊥底面ABCD ， E是A1D上一点，且A1E=2ED．
（1）求证：EO∥平面A1ABB1；
（2）求直线A1B与平面A1ACC1所成角的正弦值．
考点分析：
直线与平面所成的角；直线与平面平行的判定．
题干分析：
（1）连结A1B ，利用△AOB∽△COD得出OD/OB=1/2 ，又DE/A1E=1/2 ，故而OE∥A1B ，于是EO∥平面A1ABB1．
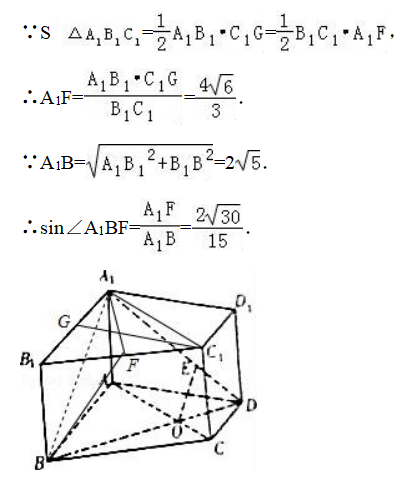
（2）过A1作A1F⊥B1C1于F ，连结BF ，则可证明A1F⊥平面BB1C1C ，于是∠A1BF是直线A1B与平面A1ACC1所成的角，求出A1F和A1B即可求出线面角的正弦值．
欲证线面平行，先证线线平行，欲证线线平行，可先证线面平行，反复用直线与平面平行的判定、性质定理，在同一题中也经常用到。