柱子|数据分析社会财富值分布情况，很有意思游戏|财富|情况|普通人|上图

最近在知乎上看到一个很有趣的问题：房间里有100个人，每人都有100元钱，他们在玩一个游戏。每轮游戏中，每个人都要拿出一元钱随机给另一个人，最后这100个人的财富分布是怎样的？
以下是三个不同的答案，请投票

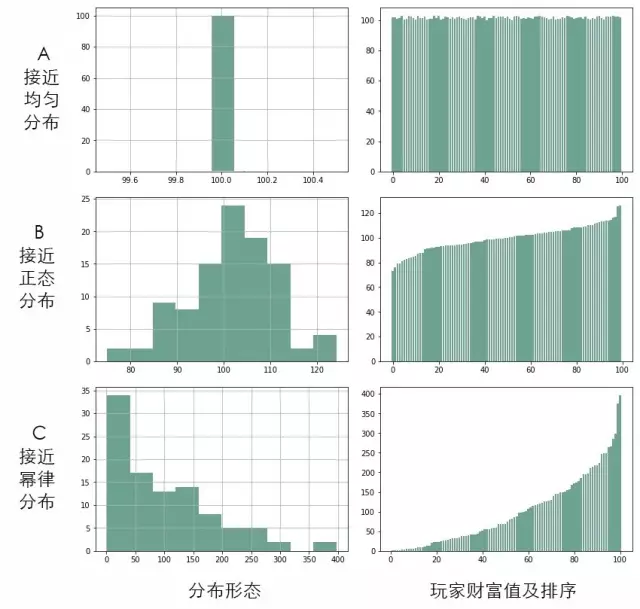
文章图片

我们不妨把这场游戏视作社会财富分配的简化模型，从而模拟这个世界的运行规律。我们假设：每个人在18岁带着100元的初始资金开始玩游戏，每天玩一次，一直玩到65岁退休。 “每天拿出一元钱”可理解为基本的日常消费， “获得财富的概率随机”是为了……嗯……简化模型。以此计算，人一生要玩17000次游戏，即获得17000次财富分配的机会。
下面我们来回答一下。
在上述规则下，游戏运行17000次的结果如下图所示：
（说明：1.上图中横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化。 2. 当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱。）
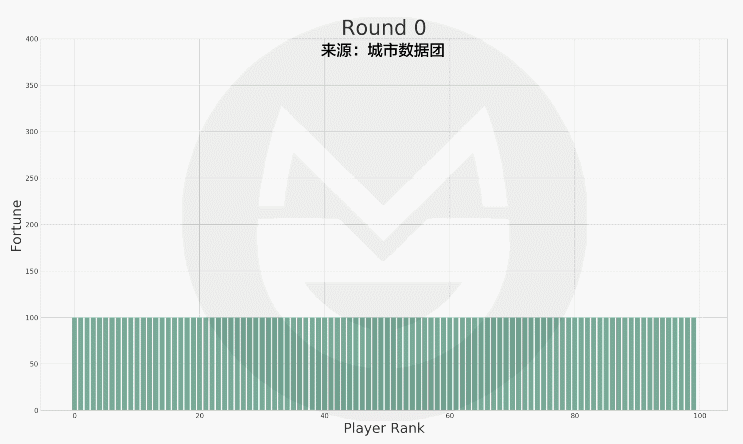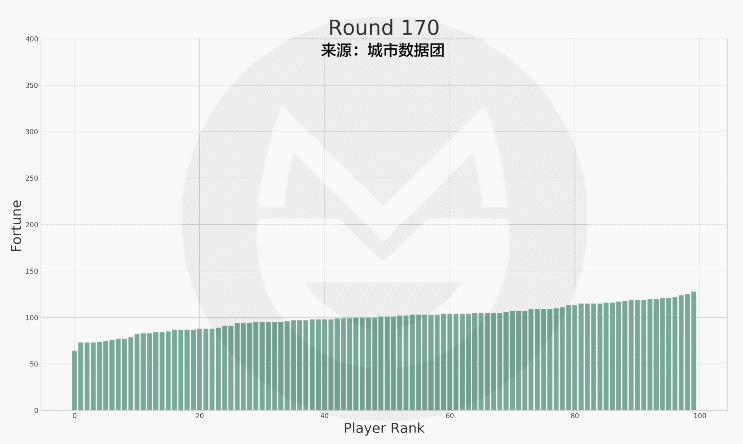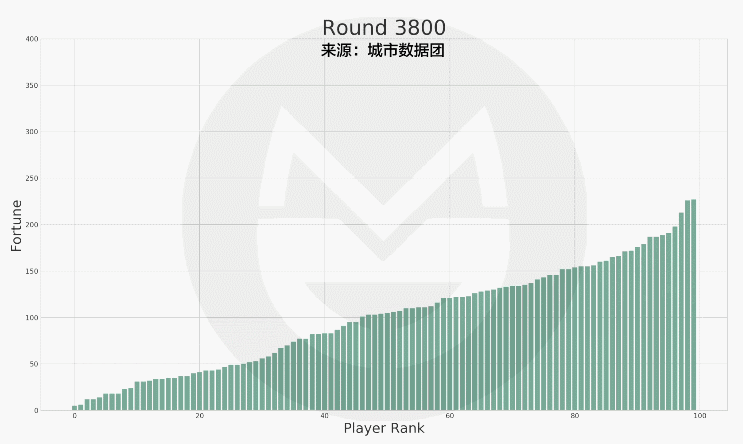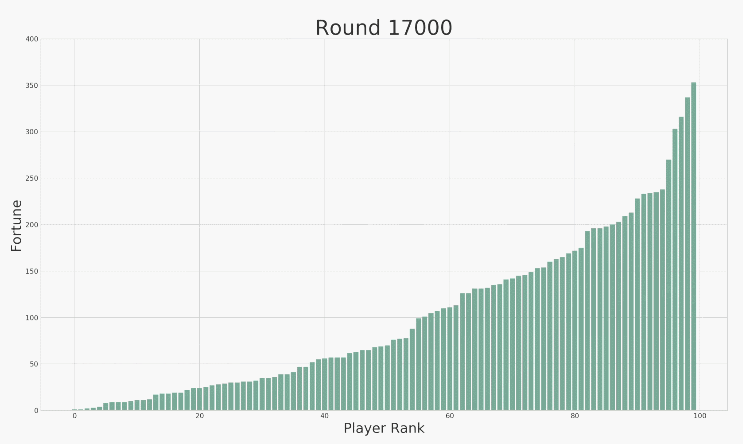
可以看到，每个玩家财富值的变动是极为剧烈的。为了方便描述整个社会财富的分配状况，我们又按照财富值的排序做了下图：

文章图片

（说明：上图中横轴标签代表玩家排序（非编号），排序越高的财富越多。初始时所有人的财富值相等，随着游戏的进行，财富值差距越来越大。）
没错，财富的分配接近于幂律分布（结论只是程序模拟，而非数学精确求解）。最后，社会将有很少的富人和很多的穷人：
就这样，大部分人的钱跑进了少部分人的口袋里。即使在最公平的规则下，世界依然展现出了残酷的一面。
在此基础上，我们又设计了更多的情景，同样用程序进行了模拟。
允许借债会让世界变得好一点吗？
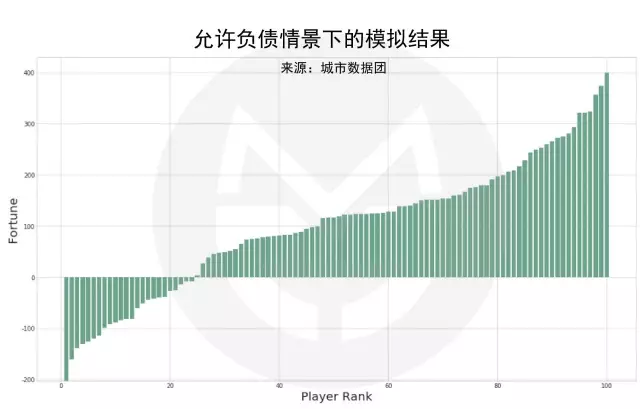
在现实社会中，情境会更复杂一些。比如说，当我们没钱了，还可以找亲友、找银行、找投资人借债，说不定哪天就东山再起了呢。在允许借债的情况下，游戏结果如下图所示（排序后结果）：

文章图片

结果表明：
没错。借债虽然能让我们在走投无路时多一些周转余地，但最终会让穷人变得更穷。
屌丝真能逆袭吗？
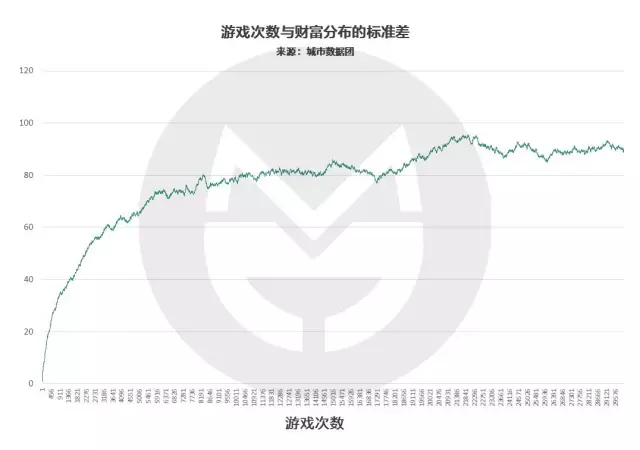
我们以所有玩家财富值的标准差来衡量社会贫富分化程度，按时间序列做出图来长这样：

文章图片

（说明：横轴表示游戏轮数，纵轴表示社会财富的标准差）
可以看到，游戏早期的标准差变动最为激烈，而在6000-6500轮游戏后，标准差的变化趋于平缓，也就是社会财富分布的总体形态趋于稳定了。按照我们设定的游戏与人生的对应规则，这时玩家年龄为35岁。
这个结果告诉我们， 35岁之前，人与人之间的差距已经完全拉开了。
进一步看，如果一个人在35岁时破产，还有没有可能逆袭呢？
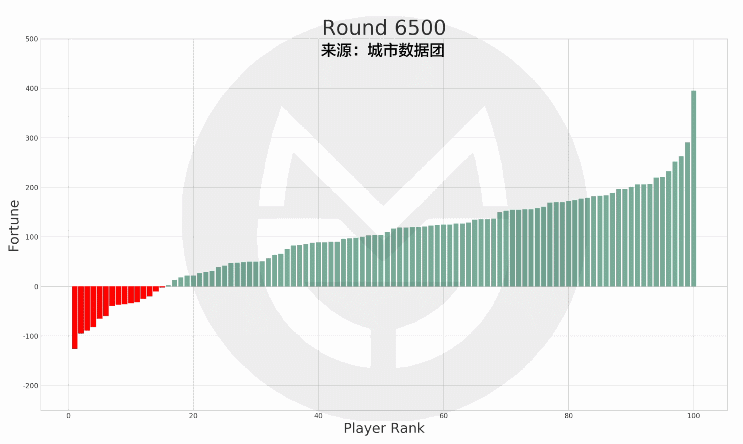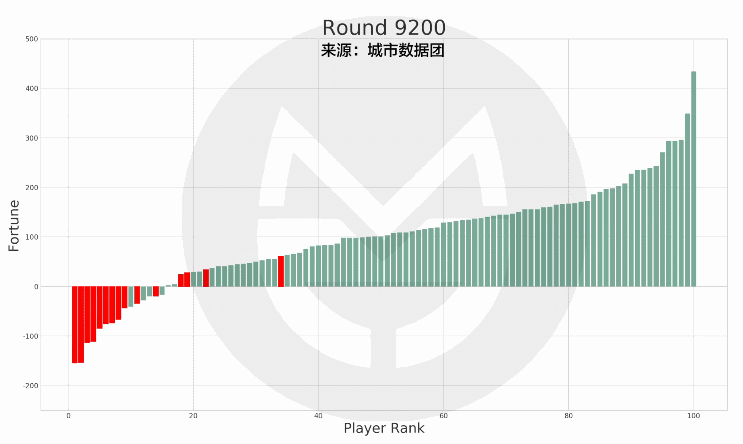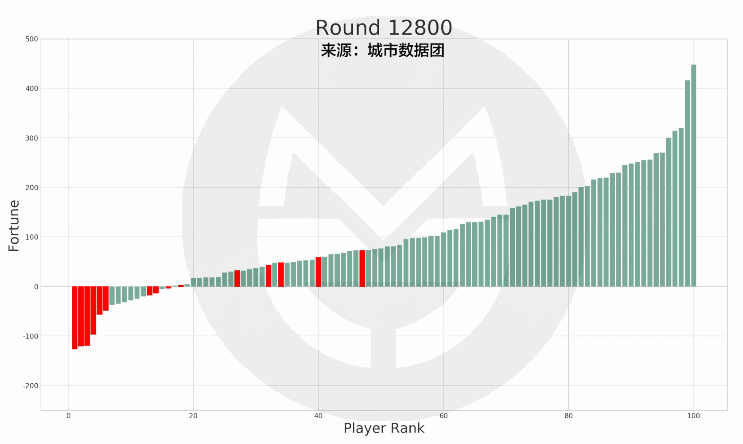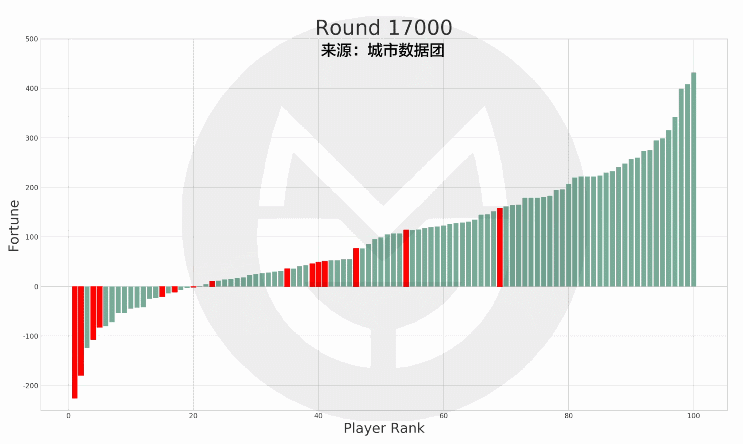
本次模拟结果中，有15个人在35岁的最后一天时处于破产（负债）状态，而他们在此后的财富值及排名如下图所示：

文章图片

（说明：上图中的红色柱子为在35岁时破产的玩家，绿色柱子为其他玩家。红色柱子在纵轴上的高度变化表示其财富值变化，在横轴上的位置变化表示其排名变化。）
可以看到，当这15个人在65岁退休时，有7人仍然处于破产状态；有8人还清债务并有了财富积累，但离富豪仍有相当差距。
看来，以35岁为界，虽然破产以后，仍有一半概率回复到普通人的生活，但想要逆袭暴富，却是相当困难的。
所以，发财要趁早，大龄屌丝逆袭更像是一个传说。
富二代和普通人有什么区别？
在真实社会中，每个人的起点其实并不相同。总有一些富二代、富三代，在财富游戏的开始就占尽了便宜。这一点也应该被考虑到我们的模型中。
为了简化计算，我们假设只有两类玩家：90个普通玩家（设定同上）+10个富二代玩家。富二代玩家的初始财富是500元，他们在每轮游戏中需要拿出2倍的钱，同时获得财富的几率也是普通人的2倍。游戏结果如下图所示（排序后结果）：