虫洞|时空是平直的，还是弯曲的？时空穿越应以何种形式实现？时空弯曲|科学|科

【虫洞|时空是平直的，还是弯曲的？时空穿越应以何种形式实现？】

打造一部机器，调节好时间地点，人站在里面一按按钮，便能够穿行于过去未来，这不过是科幻作品中天马行空般的想象罢了。
当然，这并不是说时空穿越就没有办法实现，而是说要想穿越时空，绝不会如此简单，也不会以这种形式实现。那么怎样才能穿越时空呢？时空穿越是否存在着理论基础呢？要解答心中的疑问，首先必须要弄清时空是什么。
单从字面上来理解，时空就是时间与空间，这是正确的，因为时间与空间本就是不可分割的一个整体。在人类的科学发展过程中，先后出现了两种截然不同的时空观，第一类时空观是以牛顿为代表的，他认为时空是平直的。在牛顿的理解中，时间与空间是平直的，且时间就如同一条湍急的河流，所有人置身其中，只能随波逐流一路向前，而不能倒退。

第二类时空观是以爱因斯坦为代表的，他认为时空并不是平直的，而是弯曲的，质量大的物体会改变周围时空弯曲的曲率，从而改变时间的流淌速度，如果一个人的速度够快，那么他就可以在这条时间长河之中逆流而上，穿越时空。
那么，什么是平直的时空，什么又是弯曲的时空呢？我们来举个例子，平直的时空就如同一个平面，假设在平面上有AB两个点，一个小球由A向B运动，在不受外力的作用下，它的路径将为A到B之间的连接的直线，因为这条路径是两点之间最短的距离。但弯曲的时空与此有所不同，它就如同一个球体，如果我们在一个足球的表面画上AB两个点，那么两点之间的最短距离是什么呢？连接AB两点的直线？不对。要在球体表面找到两点之间的最短距离，情况有些复杂。

要以球心作为圆心，经过AB两点画一个圆，然后连接AB两点之间的弧线就是两点的最短距离，物体在不受外力作用的情况下，从A到B也会沿着这条路径前进。
在球面上是如此，在弯曲的时空中也是如此。众所周知，太阳作为一个大质量的天体会导致周围时空发生弯曲，而地球围绕太阳运动的路径恰好就是按上述计算方法计算而出的在弯曲表面运动的最短路径。与球面不同的是，弯曲的不仅仅是空间，还有时间，在弯曲的时空中，任何物体都拥有四个坐标，前三个坐标锚定了空间位置，最后一个坐标则表示时间。在平直的时空观之下，穿越时空是不可能实现的，但是在弯曲的时空观下，穿越时空就有了理论上的可能性，那么时空穿越到底应以何种形式来实现呢？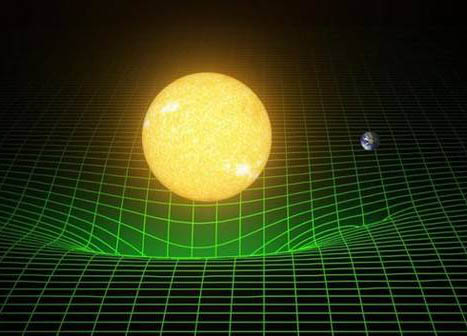

有一种理论上的时空穿越方法是由数学家提普勒所提出的，他以弯曲的时空观为基础，既然时空是弯曲的，且物体的质量越大，周围时空弯曲的曲率就越高，那么问题就很简单了，只需要建造一个圆柱就可以实现时空穿越了，这个圆柱又被叫做提普勒圆柱。
提普勒圆柱要满足三个条件，第一，拥有无限的长度，第二，拥有极高的密度，第三，高速转动，此时只需要站在这个圆柱体周围就可以因为时空的极度弯曲而实现时空穿越。提普勒的时空穿越方法在理论上基本上是完美的，但也仅仅是在理论上而已，因为要打造一个拥有无限长度的圆柱是不可能的，因为宇宙空间本身就是有限的，怎么可能在有限的空间中打造一个无限长的圆柱体呢？所以提普勒所只是在数学层面解决了时空穿越的问题。

另有一种时空穿越的方法，人们大多有所耳闻，那就是虫洞，虫洞是一种理论上存在的时空连接通路，通过虫洞不仅可以实现空间的穿越，也可以实现时间的跨越。
但虫洞只是理论上推导而出的，宇宙中是否真实存在不得而知。不过既然理论上可以推导出虫洞，那么就说明虫洞有成为现实的基础，那么我们是否可以人工打造虫洞呢？可以是可以，不过在理论上要想打开虫洞就必须要具备一种物质，这种物质要拥有负质量以及负能量，这是一种很奇妙的属性，是迄今为止人类都没有发现过的东西，所以科学家们将这种东西称之为奇异物。然而就算未来科学家找到奇异物，打开了虫洞，但是要想借助虫洞完成时空穿越也并不容易，因为通过理论计算可知，虫洞两端的张力足以将任何物质撕得粉碎。