数据结构与算法系列 - 深度优先和广度优先( 二 )
- 二叉树模版
//C/C++//递归写法:map visited;void dfs(Node* root) {// terminatorif (!root) return ;if (visited.count(root->val)) {// already visitedreturn ;}visited[root->val] = 1;// process current node here.// ...for (int i = 0; i < root->children.size(); ++i) {dfs(root->children[i]);}return ;} Python 版本#Pythonvisited = set() def dfs(node, visited):if node in visited: # terminator# already visitedreturnvisited.add(node)# process current node here....for next_node in node.children():if next_node not in visited:dfs(next_node, visited)C/C++ 版本//C/C++//递归写法:map visited;void dfs(Node* root) {// terminatorif (!root) return ;if (visited.count(root->val)) {// already visitedreturn ;}visited[root->val] = 1;// process current node here.// ...for (int i = 0; i < root->children.size(); ++i) {dfs(root->children[i]);}return ;} JavaScript版本visited = set() def dfs(node, visited):if node in visited: # terminator# already visitedreturnvisited.add(node)# process current node here....for next_node in node.children():if next_node not in visited:dfs(next_node, visited)- 多叉树模版
visited = set() def dfs(node, visited):if node in visited: # terminator# already visitedreturnvisited.add(node)# process current node here....for next_node in node.children():if next_node not in visited:dfs(next_node, visited)非递归写法Python版本#Pythondef DFS(self, tree):if tree.root is None:return []visited, stack = [], [tree.root]while stack:node = stack.pop()visited.add(node)process (node)nodes = generate_related_nodes(node)stack.push(nodes)# other processing work...C/C++版本//C/C++//非递归写法:void dfs(Node* root) {map visited;if(!root) return ;stack stackNode;stackNode.push(root);while (!stackNode.empty()) {Node* node = stackNode.top();stackNode.pop();if (visited.count(node->val)) continue;visited[node->val] = 1;for (int i = node->children.size() - 1; i >= 0; --i) {stackNode.push(node->children[i]);}}return ;} 遍历顺序我们看深度优先搜索或者深度优先遍历的话 , 它的整个遍历顺序毫无疑问根节点 1 永远最先开始的 , 接下来往那个分支走其实都一样的 , 我们简单起见就是从最左边开始走 , 那么它深度优先的话就会走到底 。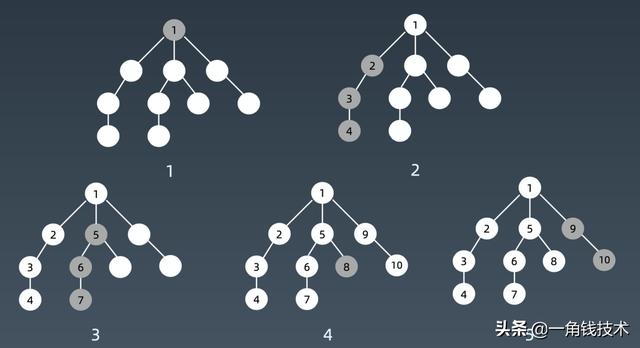 文章插图
文章插图参考多叉树模版我们可以在脑子里面或者画一个图把它递归起来的话 , 把递归的状态树画出来 , 就是这么一个结构 。
- 就比如说它开始刚进来的话 , 传的是 root 的话 , root 就会先放到 visited 里面 , 表示 root 已经被 visit,被 visited之后就从 root.childern里面找 next_node , 所有它的next_node都没有被访问过的 , 所以它就会先访问最左边的这个结点 , 这里注意当它最左边这个结点先拿出来了 , 判断没有在 visited里面 , 因为除了 root之外其他结点都没有被 visited过 , 那么没有的话它就直接调dfs , next_node 就是把最左边结点放进去 , 再把 visited也一起放进去 。
- 递归调用的一个特殊 , 它不会等这个循环跑完 , 它就直接推进到下一层了 , 也就是当前梦境的话这里写了一层循环 , 但是在第一层循环的时候 , 我就要开始下钻到新的一层梦境里面去了 。
 文章插图
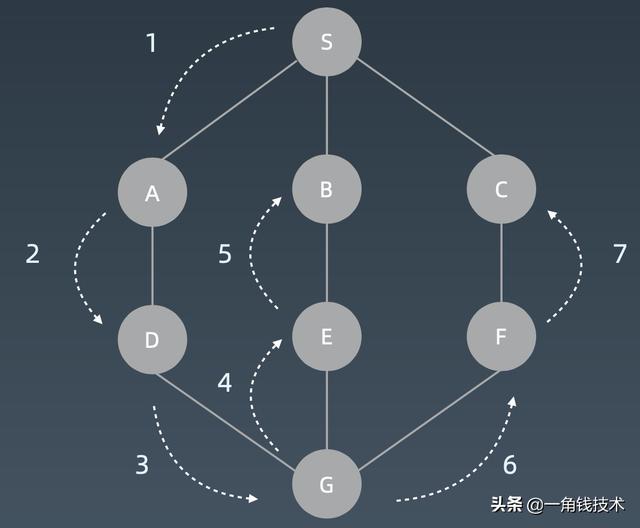
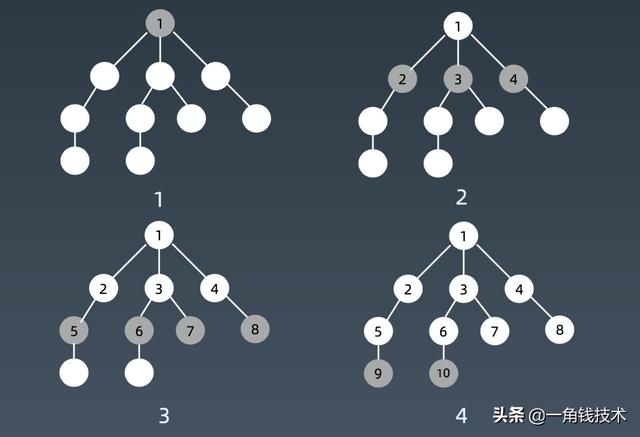
文章插图广度优先搜索(BFS)广度优先遍历它就不再是用递归也不再是用栈了 , 而是用所谓的队列 。 你可以把它想象成一个水滴 , 滴到1这个位置 , 然后它的水波纹一层一层一层扩散出去就行了 。
 文章插图
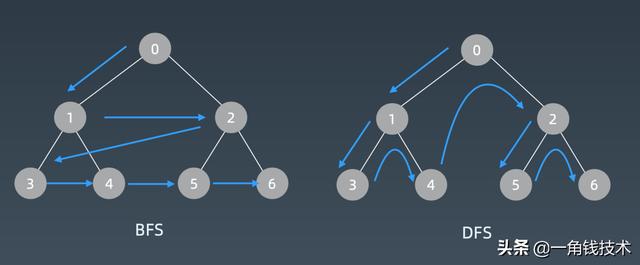
文章插图两者对比
 文章插图
文章插图BFS代码模板
//Javapublic class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}}public List> levelOrder(TreeNode root) {List> allResults = new ArrayList<>();if (root == null) {return allResults;}Queue nodes = new LinkedList<>();nodes.add(root);while (!nodes.isEmpty()) {int size = nodes.size();List results = new ArrayList<>();for (int i = 0; i < size; i++) {TreeNode node = nodes.poll();results.add(node.val);if (node.left != null) {nodes.add(node.left);}if (node.right != null) {nodes.add(node.right);}}allResults.add(results);}return allResults;} # Pythondef BFS(graph, start, end):visited = set()queue = []queue.append([start])while queue:node = queue.pop()visited.add(node)process(node)nodes = generate_related_nodes(node)queue.push(nodes)# other processing work...
- 创意|wacom one万与创意数位屏测评
- 逛逛|淘宝内容化再升级:“买家秀”变身“逛逛”试图冲破算法局限
- 黑莓(BB.US)盘前涨逾32%,将与亚马逊开发智能汽车数据平台|美股异动 | US
- 巅峰|realme巅峰之作:120Hz+陶瓷机身+5000mAh 做到了颜值与性能并存
- 抖音小店|抖音进军电商,短视频的商业模式与变现,创业者该如何抓住机遇?
- YFI正式宣布与Sushiswap合作|金色DeFi日报 | 合作
- 小店|抖音小店无货源是什么?与传统模式有什么区别?
- 星期一|亚马逊:黑五与网络星期一期间 第三方卖家销售额达到48亿美元
- 迁徙|网红迁徙记:哪里才是奶与蜜之地?
- 与用户|掌握好这4个步骤,实现了规模性的盈利
