偏导数在并联电路（并联电阻）中的一个巧妙应用偏导数是多元微积分中最基础

偏导数是多元微积分中最基础的内容，但也特别实用，如下就是在电子电路中的一个巧妙应用
首先来回顾下偏导数的定义
定义对于X的偏导数
竖直平面y=y0割曲面Z=f(x,y)得到曲线z=f(x,y0) ，这条曲线是在平面y=y0内函数z=f(x,y0)的图形，它的水平坐标是x ，竖直坐标是z ，我们定义f在点(x0,y0)对x的偏导数是f(x,y0)在点x=x0对于x的普通导数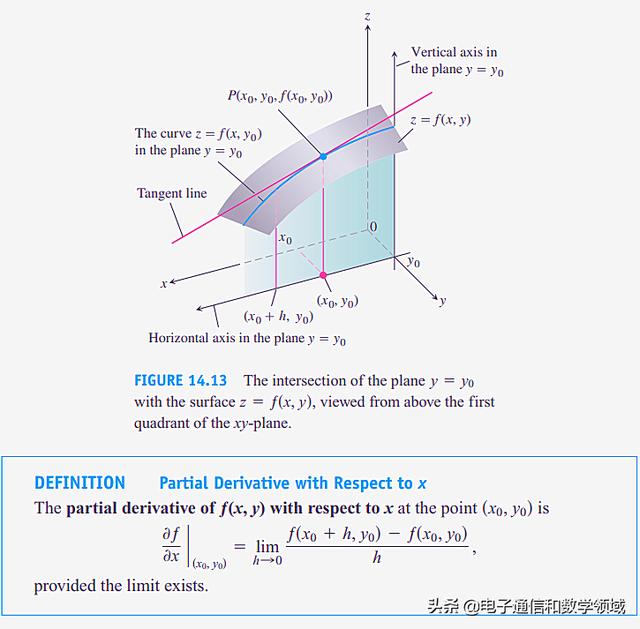
文章插图
定义对于y的偏导数
【偏导数在并联电路（并联电阻）中的一个巧妙应用】那么在点(x0,y0)对于y的偏导数的定义类似于f对于x的偏导数，这时我们把x固定在x0的值，而取f(x0,y)在y0对于y的普通导数
文章插图
我们都知道并并联联电阻的公式：如下R1,R2,R3欧姆的电阻并联成R欧姆的电阻， R值就是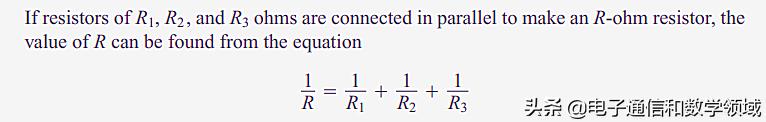
文章插图
现在我们想知道这三个电阻当中任意一个阻值的变化会对总电阻R产生什么样的影响，比如R2变化时，它对R的影响就要用到偏导数的基本知识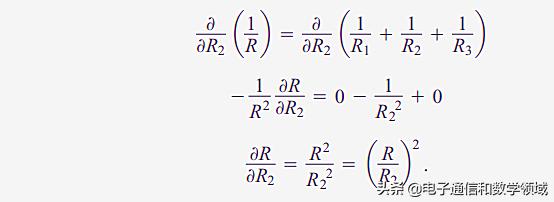
文章插图
同理对于R1,R3 ，其结果就是(R/R1)^2,(R/R3)^2
假设R1=30,R2=45,R3=90时，总电阻R=15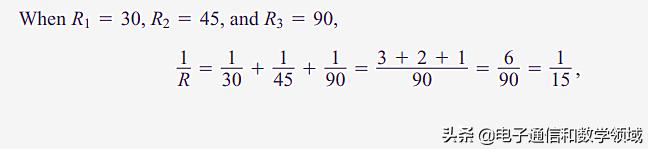
文章插图
所以R相对于R2的变化率就是1/9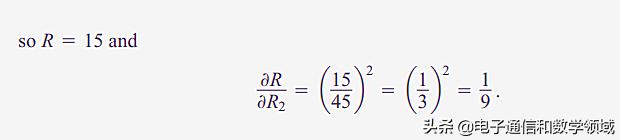
文章插图
这里有一个非常重要的结论：因为这个三个电阻对总电阻的变化率是(R/R1)^2,(R/R2)^2 ， (R/R3)^2 ，总的R不变时， R1,R2,R3中越小的对总电阻R影响越大， R1,R2,R3中越大的对总电阻R影响越小。所以设计电路的朋友要特别注意。