介绍神经网络背后的数学

文章插图
> Created by Author using Diagrams.Net
让我们深入了解神经网络和深度学习背后的数学如今，借助TensorFlow ， Keras或PyTorch之类的开源机器学习软件库，即使结构复杂度很高，也只需几行代码就可以创建神经网络。话虽如此，神经网络背后的数学仍然是我们中某些人的谜团，拥有神经网络和深度学习背后的数学知识可以帮助我们了解神经网络内部正在发生的事情。它还在架构选择，深度学习模型的微调，超参数调整和优化方面有帮助。
介绍由于我不太了解代数或微积分，所以很长一段时间以来，我一直忽略了对神经网络和深度学习背后的数学的理解。几天前，我决定从头开始，并推导神经网络和深度学习背后的方法论和数学，以了解它们如何工作以及为什么起作用。我还决定写这篇文章，这对像我这样的人非常有用，他们觉得很难理解这些概念。
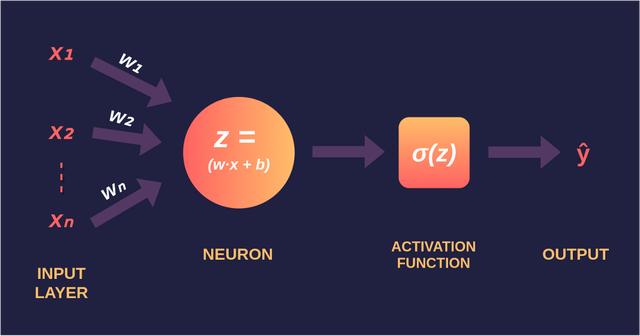
感知器感知器-由弗兰克·罗森布拉特（Frank Rosenblatt）于1958年发明的，是最简单的神经网络，由n个输入，一个神经元和一个输出组成，其中n是数据集的特征数量。将数据通过神经网络传递的过程称为前向传播，并在以下三个步骤中说明了在感知器中执行的前向传播。
步骤1：对于每个输入，将输入值x?与权重w?相乘，然后将所有相乘后的值相加。权重-代表神经元之间连接的强度，并决定给定输入将对神经元输出产生多大影响。如果权重w 1的值大于权重w 2 ，则输入x 1对输出的影响将大于w 2 。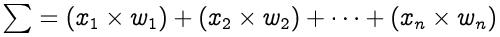
文章插图
输入和权重的行向量分别为x = [x? ， x 2 ， … ， x?]和w = [w? ， w 2 ， … ， w?] ，其点积由下式给出：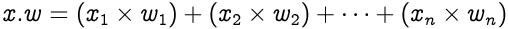
文章插图
因此，总和等于向量x和w的点积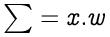
文章插图
第2步：将偏差b加到相乘值的总和上，我们称之为z 。偏移-在大多数情况下，也需要偏移，以将整个激活功能向左或向右移动以生成所需的输出值。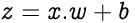
文章插图
步骤3：将z的值传递给非线性激活函数。激活函数-用于将非线性引入神经元的输出中，否则，神经网络将只是线性函数。而且，它们对神经网络的学习速度有重大影响。感知器具有二进制步进功能作为其激活功能。但是，我们将使用sigmoid（也称为逻辑函数）作为激活函数。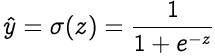
文章插图
其中σ表示S型激活函数，而在正向授权后获得的输出称为预测值。
学习算法学习算法由两部分组成-反向传播和优化。
反向传播：反向传播，是错误的向后传播的缩写，是指用于计算损失函数相对于权重的梯度的算法。但是，该术语通常用于指整个学习算法。以下两个步骤说明了在感知器中进行的反向传播。
第1步：要知道我们与所需解有多远的估计，使用了损失函数。通常，对于回归问题，选择均方误差作为损失函数；对于分类问题，选择均方误差作为交叉熵。让我们来看一个回归问题，其损失函数为均方误差，即均方根（y?）与预测值（??）之间的差。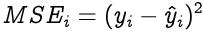
文章插图
针对整个训练数据集计算损失函数，其平均值称为成本函数C 。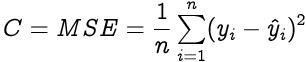
文章插图
步骤2：为了为我们的感知器找到最佳的权重和偏差，我们需要知道成本函数相对于权重和偏差如何变化。这是借助梯度（变化率）完成的-一个量相对于另一个量如何变化。在我们的案例中，我们需要找到成本函数相对于权重和偏差的梯度。
让我们使用偏导数计算成本函数C相对于权重w?的梯度。由于成本函数与权重w?没有直接关系，因此我们使用链式规则。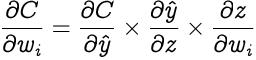
文章插图
【介绍神经网络背后的数学】现在我们需要找到以下三个渐变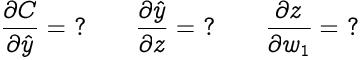
文章插图
让我们从成本函数（C）相对于预测值（）的梯度开始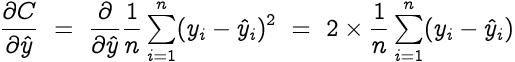
文章插图