力扣LeetCode 32最长有效括号(困难)
维护不易 , 还请点个赞赞 , 如果想加入打卡还请关注公众号bigsai回复进群加入打卡 。
题目描述给定一个只包含 ‘(’ 和 ‘)’ 的字符串 , 找出最长的包含有效括号的子串的长度 。
【力扣LeetCode 32最长有效括号(困难)】示例 1:
输入: “(()”输出: 2解释: 最长有效括号子串为 “()”
示例 2:
输入: “)()())”输出: 4解释: 最长有效括号子串为 “()()”
分析再看这题之前 , 咱们回顾一下前面刷过的题 。 力扣20有效的括号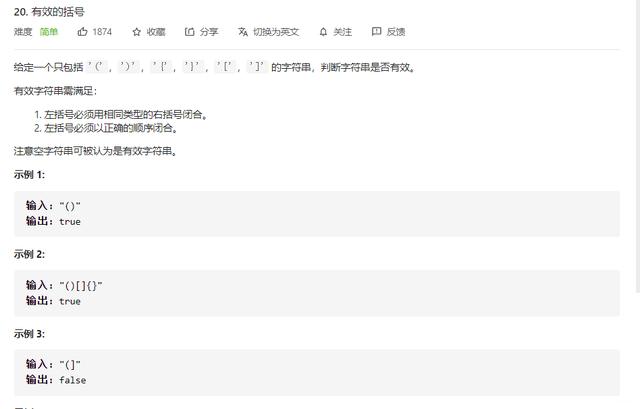 文章插图
文章插图
分析这种题核心思想就是使用栈模拟 。 本题的话更简单一点因为只有(和 )两种括号 , 只有两个东西的话很多时候可以省略很多内容 。 在使用暴力的时候就可以循环每次找到最长的有效括号 。 而括号匹配的时候可以直接终止的情况是当前多个)右括号 。 例如())(到第三个不可能和前面相连 , 而如果来(只需要期待后面能够来) 。 一个)可以和一个(组成一对 , 消除栈中的一个( 。
当然 , 在具体的实现上 , 我们用数组模拟栈 , 实现代码为:
publicint longestValidParentheses(String s) { char str[]=s.toCharArray();//字符数组 int max=0; for(int i=0;i=str.length-i)break;for(int j=i;j尽管有一些地方有优化空间 , 比如剪枝把各种不可能的给剪掉 , 但整个算法还是太复杂 , 算法的复杂度为O(n2).并且只击败5%的人 , 所以在这方面宣告算法宣告失败: 文章插图
文章插图
其实这个暴力是昨晚睡觉前过的 ,因为我看到困难级别我在刷的时候用暴力过了好歹我也是过了 , 过了之后上床之后我就在想怎么去优化这道题 。
在今天早上的时候用笔画了画想了想成功攻破该题(看不懂不要紧 , 下面给你慢慢讲): 文章插图
文章插图
如何将这道题从一个O(n2)的时间复杂度优化到O(n)?很容易 ,我们需要注意他的过程 。 我们先随便看几个可能的最大情况 。
对于这么一次获取你会发现不同括号会有些区别:(:左括号一旦出现那么他就期待一个)进行匹配 , 但它的后面可能有)并且在这中间有很多其他括号对 。 ):右括号有两种情况:
在具体实现的思路上 , 就是使用一个int数组标记当前层级(栈深)有正确的括号数量 。模拟一次栈行为从左向右 , 遇到)太多(当前栈中不存在(进行匹配)就将数据清零重新开始 。 这样一直到最后 。 你可以把它看成台阶 , 遇到(就上一个台阶并清零该新台阶 , 遇到)就下一个台阶并且把数量加到下降后的台阶上 。 具体可以看下面图片模拟呃过程:( ) ( ( ) ( ) ( ( ) ) )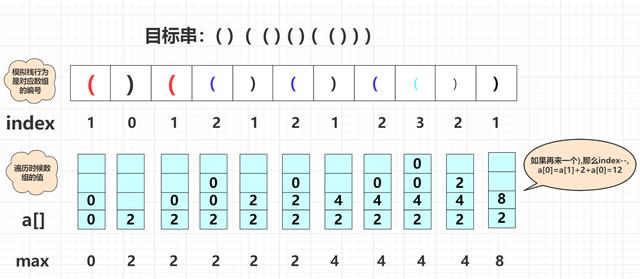 文章插图
文章插图
仔细看看这张图 , 具体实现代码为:
public static int longestValidParentheses(String s) {int max=0;int value[]=new int[s.length()+1];int index=0;for(int i=0;imax)//更新max=value[index];}}}return max;} 文章插图
文章插图
好啦 , 这个O(n)的复杂度还行 , 至于其他解法也没研究有空可以看看 。 这次打卡就结束啦 , 如果有兴趣的欢迎关注公众号bigsai 回复进群 , 加入打卡!一起刷题 。
还请点赞、关注支持一下 。
- LeetCode第1 题:两数之和 Go语言精解
- leetcode之最短补全词
- leetcode之有多少小于当前数字的数字
- 程序员面试题:Leetcode真题讲解,求两数之和
- 跨境电商拉开序幕,综合电商也要来分一杯羹|史上最长“黑五”·交锋| 考拉海购
- 真假难辨、运费高、清关慢……跨境电商怎么破?|史上最长“黑五”·大考 | 跨境
- 内置|续航时间最长的5部5G手机:小米拿到第一,网友:大电池就是好
- Apple Music年终福利来袭 可免费试用最长达五个月
- leetcode之Bigram分词
- leetcode之字符串压缩
