嵌入|图嵌入概述作者：rimo?Godec编译：ronghuaiy

作者：rimo? Godec
编译：ronghuaiyang
导读这篇文章描述了什么是图嵌入，图嵌入的用处，并对比了常用的几种图嵌入方法。
文章插图
【嵌入|图嵌入概述】图常用在现实世界的不同场景中。社交网络是人们相互联系的大型图，生物学家使用蛋白质相互作用的图，而通信网络本身就是图。他们在文本挖掘领域使用词共现图。对在图形上使用机器学习的兴趣正在增长。他们试图在社交媒体上预测新的联系，而生物学家预测蛋白质的功能标签。图上的数学和统计操作是有限的，将机器学习方法直接应用到图上是很有挑战性的。在这种情况下，嵌入似乎是一个合理的解决方案。
什么是图嵌入？
图嵌入是将属性图转换为一个或一组向量。嵌入应该捕获图的拓扑结构、顶点到顶点的关系以及关于图、子图和顶点的其他相关信息。更多的属性嵌入编码可以在以后的任务中获得更好的结果。我们大致可以将嵌入分为两组：
顶点嵌入：我们用每个顶点(节点)自己的向量表示对其进行编码。当我们想要在顶点层次上执行可视化或预测时，我们会使用这种嵌入，例如在二维平面上对顶点进行可视化，或者基于顶点相似性预测新的连接。
图嵌入：这里我们用一个向量表示整个图。当我们想要在图的层次上做出预测时，以及当我们想要比较或可视化整个图时，例如比较化学结构时，就会用到这些嵌入。
稍后，我们将介绍来自第一组的一些常用方法(DeepWalk、node2vec、SDNE)和来自第二组的graph2vec方法。
我们为什么要用到图嵌入？
图是一种有意义的、可理解的数据表示，但是需要使用图嵌入的原因如下：

机器学习在图上的应用是有限的。图由边和节点组成。这些网络关系只能使用数学、统计和机器学习的特定子集，而向量空间有更丰富的方法工具集。
嵌入是压缩的表示。邻接矩阵描述图中节点之间的连接。它是一个|V| x |V|矩阵，其中|V|是图中的一些节点。矩阵中的每一列和每一行都表示一个节点。矩阵中的非零值表示两个节点连接。对于大型图，使用邻接矩阵作为特征空间几乎是不可能的。假设一个图有1M个节点和一个1M x 1M的邻接矩阵。嵌入比邻接矩阵更实用，因为它们将节点属性打包到一个维度更小的向量中。
向量运算比图上的运算更简单、更快。

挑战
嵌入方法需要满足更多的需求。这里我们描述了嵌入方法面临的三个挑战：

我们需要确保嵌入能够很好地描述图的属性。它们需要表示图拓扑、节点连接和节点邻居。预测或可视化的性能取决于嵌入的质量。
网络的大小不应降低嵌入过程的速度。图通常很大。想象一下拥有数百万人的社交网络。好的嵌入方法需要在大型图上有效。
一个基本的挑战是决定嵌入维数。较长的嵌入保存了更多的信息，同时它们比排序器嵌入带来更高的时间和空间复杂度。用户需要根据需求做出权衡。在文章中，他们通常报告说，嵌入大小在128到256之间就足够完成大多数任务。在Word2vec方法中，他们选择了嵌入长度300 。

Word2vec
在介绍嵌入图的方法之前，我将讨论Word2vec方法和skip-gram神经网络。它们是图形嵌入方法的基础。
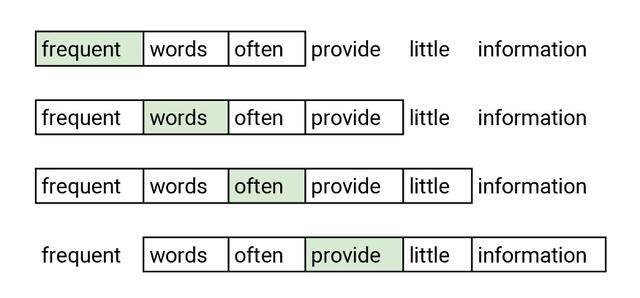
Word2vec是一种将单词转换为嵌入向量的嵌入方法。相似的单词应该有相似的嵌入。 Word2vec采用skip-gram网络， skip-gram网络具有一个隐含层的神经网络。 skip-gram被训练来预测句子中的相邻单词。这个任务被称为伪任务，因为它只是在训练阶段使用。网络在输入端接受单词，并对其进行优化，使其能够以较高的概率预测句子中的相邻单词。下图显示了输入单词(用绿色标记)和预测单词的示例。通过这个任务，作者实现了两个相似的单词具有相似的嵌入，因为具有相似含义的两个单词很可能具有相似的邻域单词。

文章插图
用绿色表示网络。优化后的算法能较好地预测邻域内的词，具有较高的预测概率。在本例中，我们考虑距离所选单词最远的两个位置的单词。
下图所示的skip-gram神经网络有输入层、隐藏层和输出层。网络接受one -hot编码。 one -hot编码是一个长度与单词字典数量相同的向量，只有一个1其他都是0 。这个1出现的位置是字典中出现编码单词的地方。隐藏层没有激活函数，它的输出是一个单词的嵌入。输出层是一个预测邻域单词的softmax分类器。