如图：
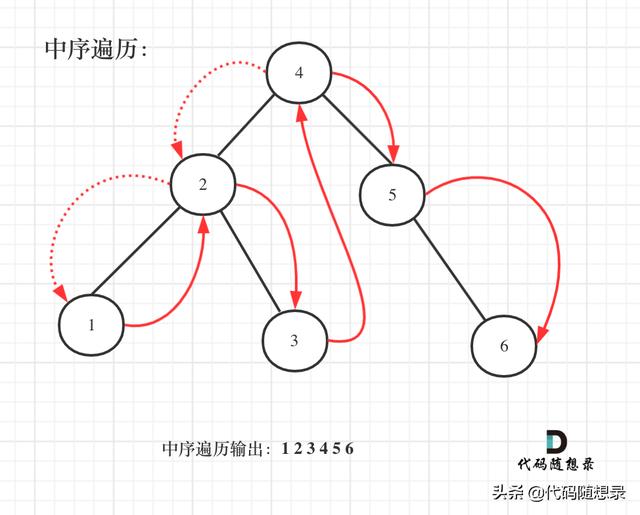文章插图
中序遍历代码如下：
void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);// 左（处理节点）// 中searchBST(cur->right);// 右return ;}遍历有序数组的元素出现频率 ， 从头遍历 ， 那么一定是相邻两个元素作比较 ， 然后就把出现频率最高的元素输出就可以了 。
关键是在有序数组上的话 ， 好搞 ， 在树上怎么搞呢？
这就考察对树的操作了 。
在二叉树：搜索树的最小绝对差 中我们就使用了pre指针和cur指针的技巧 ， 这次又用上了 。
弄一个指针指向前一个节点 ， 这样每次cur（当前节点）才能和pre（前一个节点）作比较 。
而且初始化的时候pre = NULL ， 这样当pre为NULL时候 ， 我们就知道这是比较的第一个元素 。
代码如下：
if (pre == NULL) { // 第一个节点count = 1; // 频率为1} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}pre = cur; // 更新上一个节点此时又有问题了 ， 因为要求最大频率的元素集合（注意是集合 ， 不是一个元素 ， 可以有多个众数） ， 如果是数组上大家一般怎么办？
应该是先遍历一遍数组 ， 找出最大频率（maxCount） ， 然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合 。 （因为众数有多个）
这种方式遍历了两遍数组 。
那么我们遍历两遍二叉搜索树 ， 把众数集合算出来也是可以的 。
但这里其实只需要遍历一次就可以找到所有的众数 。
那么如何只遍历一遍呢？
如果 频率count 等于 maxCount（最大频率） ， 当然要把这个元素加入到结果集中（以下代码为result数组） ， 代码如下：
if (count == maxCount) { // 如果和最大值相同 ， 放进result中result.push_back(cur->val);}是不是感觉这里有问题 ， result怎么能轻易就把元素放进去了呢 ， 万一 ， 这个maxCount此时还不是真正最大频率呢 。
所以下面要做如下操作：
频率count 大于 maxCount的时候 ， 不仅要更新maxCount ， 而且要清空结果集（以下代码为result数组） ， 因为结果集之前的元素都失效了 。
if (count > maxCount) { // 如果计数大于最大值maxCount = count;// 更新最大频率result.clear();// 很关键的一步 ， 不要忘记清空result ， 之前result里的元素都失效了result.push_back(cur->val);}关键代码都讲完了 ， 完整代码如下：（「只需要遍历一遍二叉搜索树 ， 就求出了众数的集合」）
class Solution {private:int maxCount; // 最大频率int count; // 统计频率TreeNode* pre;vector result;void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);// 左// 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}pre = cur; // 更新上一个节点if (count == maxCount) { // 如果和最大值相同 ， 放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count;// 更新最大频率result.clear();// 很关键的一步 ， 不要忘记清空result ， 之前result里的元素都失效了result.push_back(cur->val);}searchBST(cur->right);// 右return ;}public:vector findMode(TreeNode* root) {count = 0;maxCount = 0;TreeNode* pre = NULL; // 记录前一个节点result.clear();searchBST(root);return result;}};