算法题 | 你追我，如果你追到我……那就算你赢了大家好

大家好，欢迎阅读周末算法题专题。
今天选择的算法题来源于昨天同一套题中的D题，这题全场通过的人数在2600人左右。虽然通过的人数更少了一些，但是题目的难度却并没有增加很多，但是趣味度增加了。我也是第一次遇见这样的问题。
题目链接：
废话不多说，我们一起来看这题的题意。
题意我们都知道数据结构当中的树有这样一个性质，如果树当中有n个点，那么它应该由n-1条无向边组成。并且树当中是一定没有环的，如果有环的话n-1条边就不够了。
今天是说有两个人分别叫做Alice和Bob在一棵树上玩游戏，这两个人名是业内的惯例。凡是两个人玩游戏的题目，主人公的名字很多都叫Alice和Bob ，我也不知道这个惯例的由来，大家知道这么回事就好了。 Alice和Bob两人各自占据了树上的一个点，然后两个人交替移动。 Alice先手， Bob后手。
Alice每一次移动最多可以移动da距离， Bob最多可以移动db距离，两个人也可以放弃移动。假设两人都绝顶聪明每一次都会选择最佳策略，请问经过最多10^100个回合之后， Alice能否捉到Bob呢？如果可以则Alice获胜，否则Bob获胜。注意在Bob的回合，它可以经过Alice的节点，这并不会被视为捉到。
不知道为什么看到这道题的时候，总是会想起费玉清的段子，不知道你们有没有这种感觉。
文章插图
样例第一行输入一个数t ，表示测试数据的组数。
【算法题 | 你追我，如果你追到我……那就算你赢了】对于每组数据首先有5个数，分别是n, a, b, da, db 。 n表示树节点的个数， a和b表示游戏开始时a和b出生点的位置。 da和db表示Alice和Bob每回合最多移动的距离。这几个数的最大范围都是1e5 ，并且多组数据当中所有的n相加不超过1e5 。
我们来看两组样例：
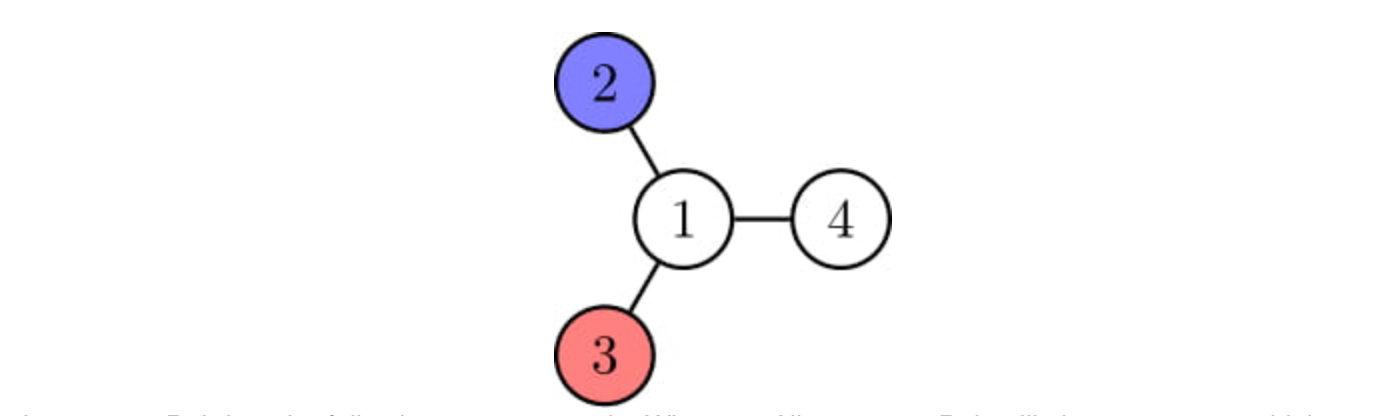
4 3 2 1 21 21 31 46 6 1 2 51 26 52 33 44 5第一组数据是这样的：
文章插图
蓝色表示Alice ，红色是Bob 。由于Alice先手，只要Alice移动到1节点，无论Bob如何移动，他都必输无疑。
第二组数据：
文章插图
由于Alice最多只能移动两格，第一回合移动到3 ， Bob选择不动。只要Alice移动，不论是一格还是两格， Bob都可以直接移动到1节点。也就是说最终Bob就在1和6节点之间来回移动，躲开Alice的追捕。
题解看到Alice和Bob两人游戏，并且两人都绝顶聪明会选择最佳策略，首先想到的就是博弈论。但是观察一下你会发现这题和博弈论没有什么关系，因为博弈论往往都是公平博弈，局面会有状态转移。但这题当中不是，这题不存在胜负状态转移，一定会有一个确定的结果，就是是谁胜谁负，所以这题不满足博弈论的前提。
类似博弈论的题面只是障眼法而已，如果你信了，并且真的往这方面努力，那么你就被出题人骗了。不过这个陷阱还是比较明显的，很容易看出来。接下来我们又遇到了另外一个陷阱，这个陷阱也很明显，就是执行的回合数量。题目给的是1e100 ，这个数是真正的天文数字，比宇宙当中所有的粒子数都要多。所以我们可以完全可以理解成无限游戏。
如果出题人阴险一点，完全可以给一个1e7这个量级的回合数，会更有欺骗性一些。其实我们想一下就会发现，树上节点最多只有1e5个，当它们玩追逐游戏的时候，只会有两种情况，一种是永远也追不上，还有一种是很快就追上。所以这个回合数没什么意义，就是唬人的。