1 说明
=====
1.1 pydotplus是旧pydot项目的一个改进版本 ， 它为graphviz的点语言提供了一个python接口 。
1.2 复习一下：
1.2.1 pydot已经淘汰了 ， 不再更新了 。
1.2.2 Dot是开源工具包Graphviz上用来画图的一门脚本语言 ， 本次不介绍了 。
1.3 提到基本绘制图形 ， dot语法类似 ， 泰坦尼克号决策树的可视化；讲解清楚 ， 注释仔细 ， 通俗易懂 ， 适合收藏 。
文章插图
2 介绍
=====
2.1 官网：
2.2 安装：
pip install pydotplus#本机安装sudo pip3.8 install pydotplus2.3 有时候可能需要安装graphviz：
pip install graphviz#注意环境变量设置3 效果展示
========
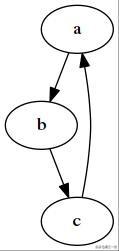
3.1 入门级图1
文章插图
3.2 图1代码：
import pydotplus as pdp#方法一 ， 单引号#graph = pdp.graph_from_dot_data('digraph demo1{a -> b -> c; c ->a; }')#方法二 ， 双引号graph = pdp.graph_from_dot_data('''digraph demo1{a -> b -> c; c ->a; }''')#生成jpg图片#graph.write_jpg('/home/xgj/Desktop/pydotplus/3dot.jpg')#生成png图片graph.write_png('/home/xgj/Desktop/pydotplus/3dot.png')#生成pdf文件#graph.write_pdf('/home/xgj/Desktop/pydotplus/3dot.pdf')3.3 图2
文章插图
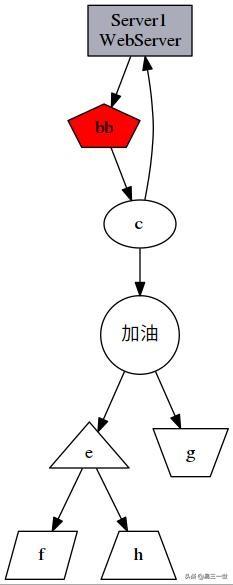
3.4 图2代码
import pydotplus as pdp#语法符合原dot语法dot = '''//定义节点属性digraph g {//==========定义节点关系============a->b;b->c;c->a;c->d->e->f;d->g;e->h;//==========定义节点属性============//定义a节点为长方形, 样式为填充, 填充颜色为#ABACBAa[shape=box,label="Server1\nWebServer",fillcolor="#ABACBA",style=filled];//定义b为5边形, 标签为"bb", 样式为填充, 填充色为redb[shape=polygon,sides=5,label="bb",style=filled,fillcolor=red];//c, 默认为椭圆d[shape=circle,label="加油",fontname="Microsoft YaHei"]; //圆e[shape=triangle]; //三角形f[shape=polygon, sides=4, skew=0.5]; //平行四边形g[shape=polygon, distortion=0.5]; //梯形, 上边长h[shape=polygon, distortion=-.5]; //梯形, 下边长}'''graph = pdp.graph_from_dot_data(dot)graph.write_jpg('/home/xgj/Desktop/pydotplus/4dot.jpg')3.5 图3
文章插图
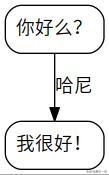
3.6 图3代码：
import pydotplus as pdpdot_cn = """digraph demo{node [shape=box, style="rounded", color="black", fontname="Microsoft YaHei"];edge [fontname="Microsoft YaHei"];a -> b[label="哈尼"]a[label="你好么？"]b[label="我很好！"]}"""graph = pdp.graph_from_dot_data(dot_cn)graph.write_jpg('/home/xgj/Desktop/pydotplus/5dot.jpg')4 泰坦尼克号的决策树
=================
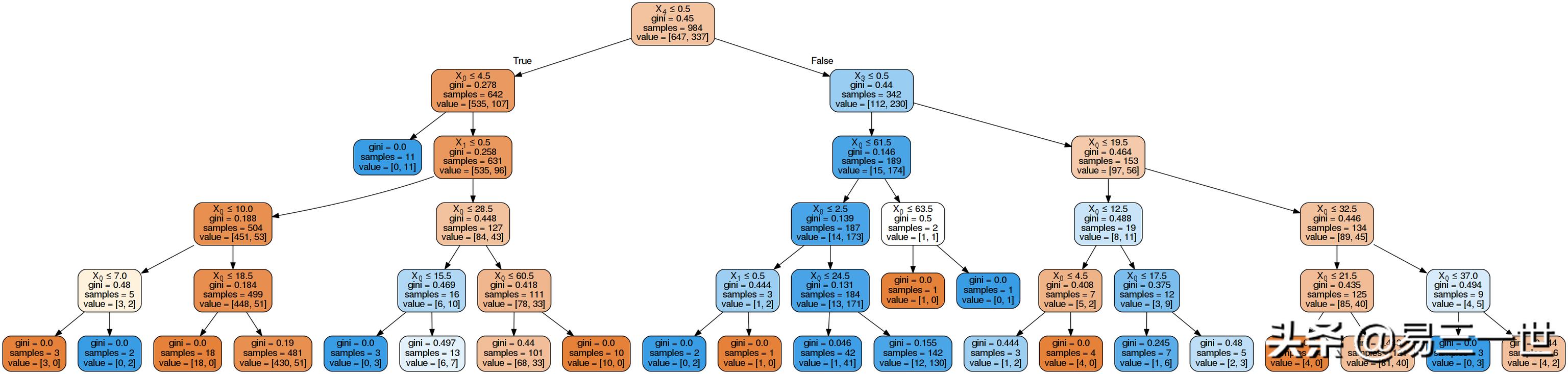
4.1 效果图
文章插图
4.2 注意
======
4.2.1 决策树是机器学习中一个比较重要而且常用的算法, 是基于香农的信息论计算信息熵然后计算信息增益 。
4.2.2 参考文章：
#;depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.add_param_isCf