你在享受十一长假时,Python 已悄悄地变了
 文章插图
文章插图
Python 3.9 在经历了将近一年的试用期后 , 于 10月5日(2020年)发布了稳定版 , 意味着 , 在下一版本发布之前 , 不会在做改动 , 童鞋们可以放心大胆地更新了 。 享受完惬意的十一长假后 , 我们快来看看新版本带来了哪些惊喜
先附上一个 16 岁印度小哥哥整理的特性图:
 文章插图
文章插图
节能篇这次版本最喜人的特性事节能 , 不仅节省电能 , 更重要的是节省了敲代码的次数 , 以及我们宝贵的时间
字典的合并与更新毫无疑问 , 字典对象(Dict)是日常编程中最常用到的数据结构 , 从存储键值对到支持复杂算法 , 都依赖于字典对象 , 而且常用一些字段的合并、更新等操作 , 虽然 Python 中已经提供了字段更新的方法和字典展开操作符( ** ) , 但是仍然不够简洁 , 我理解 , 在你看到新版本中的更新之前 , 不会感觉有什么不简洁的
原来的合并:
d1 = {'a': 'A', 'b': 'B', 'c': 'C'}d2 = {'d': 'D', 'e': 'E'}d3 = {**d1, **d2}# 使用展开操作符 , 将合并结果存入 d3print(d3)# {'a': 'A', 'b': 'B', 'c': 'C', 'd': 'D', 'e': 'E'}d1.update(d2)# update 方法 , 将 d1 d2 合并 , 且更新 d1print(d1)# {'a': 'A', 'b': 'B', 'c': 'C', 'd': 'D', 'e': 'E'}现在的合并:
d1 = {'a': 'A', 'b': 'B', 'c': 'C'}d2 = {'d': 'D', 'e': 'E'}d3 = d1 | d2# 效果等同于展开操作符print(d3)# {'a': 'A', 'b': 'B', 'c': 'C', 'd': 'D', 'e': 'E'}d1 |= d2# 等同于 updateprint(d1)# {'a': 'A', 'b': 'B', 'c': 'C', 'd': 'D', 'e': 'E'}
- | 操作符 , 除了对数值的 与 操作之外 , 现在还可以做字典对象的合并
- |= 如果要用合并的结果更新前面的字典对象 , 在合并操作符后加赋值号就行
这还没完 , 合并赋值操作符( |= )除了字典之间的合并 , 还可以合并类字典对象
先看一段代码:
d1 = {'a': 'A', 'b': 'B', 'c': 'C'}l1 = [('d', 'D'), ('e', 'E')]d1 |= l1print(d1)# {'a': 'A', 'b': 'B', 'c': 'C', 'd': 'D', 'e': 'E'}- l1 是一个列表对象 , 其中的元素是二维元组
- 这里的特别之处在于二维元组对象 , 合并时 , 第一个元素被看成字典的 Key , 第二个被看成字典的 Value , 如果不是这样 , 则会报错
拓扑排序首先需要理解什么是拓扑图 , 简单来说就是一定空间内若干个点之间的关系 , 例如对于一项工作来说 , 包含有若干个任务 , 任务之间有相互依赖的关系 , 任务加上它们之间的关系 , 就构成了一个拓扑结构图
拓扑排序 , 就是对一个拓扑图中的点按照点之间的相互关系的一种排序
例如这样一个拓扑图
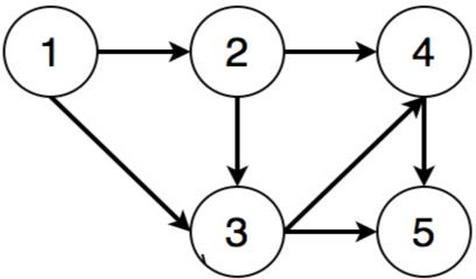 文章插图
文章插图拓扑排序为
1、2、3、4、5
如果用算法生写的话 , 需要十行以上 , 而且还不包括调试时间 , 以及为各种适应性做的改善所花的时间
现在 , 排序只需要一行代码:
from graphlib import TopologicalSortertg = {5: {3, 4}, 4: {2, 3}, 3: {2, 1}, 2: {1}}ts = TopologicalSorter(tg)print(list(ts.static_order())) # [1, 2, 3, 4, 5]static_order实际上最核心的就是创建排序对象的代码 , 新特性提供了优雅的封装
- 终于不是14nm了,英特尔十一代新品曝光
- 十一出门旅行?不,我要在家享受解放双手的日子
- 双十一临近“薅羊毛”产业链让商家闻风丧胆
- 双十一购买手机需要注意哪些?看完这些,再被坑!只能怪自己了
- 当贝投影D3X抢先体验:降温了,被窝福利安排上
- 微信又添加新表情啦!被戏称为“打工人”表情包,你在用了吗?
- 京东双十一手机销量榜:iPhone12未进前十,第一无人能敌
- 关注抽免单,美商海盗船天猫旗舰店双十一大狂欢
- 两大平台同步进行,华硕主板双十一大促活动来了
- 马云的预言或将再次应验,这4大职业未来将失业,你在其中吗?
