生活_傻大方

  1. 首页 > 人文 > >

十大经典排序算法（动图演示）( 三 )

  • 从数列中挑出一个元素 ， 称为 “基准”（pivot）；
  • 重新排序数列 ， 所有元素比基准值小的摆放在基准前面 ， 所有元素比基准值大的摆在基准的后面（相同的数可以到任一边） 。 在这个分区退出之后 ， 该基准就处于数列的中间位置 。 这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序 。
6.2 动图演示6.3 代码实现 1 function mergeSort(arr) { 2varlen = arr.length; 3if(len < 2) { 4returnarr; 5} 6varmiddle = Math.floor(len / 2), 7left = arr.slice(0, middle), 8right = arr.slice(middle); 9returnmerge(mergeSort(left), mergeSort(right));10 }1112 function merge(left, right) {13varresult = [];1415while(left.length>0 18} else{19result.push(right.shift());20}21}2223while(left.length)24result.push(left.shift());2526while(right.length)27result.push(right.shift());2829returnresult;30 }7、堆排序（Heap Sort）堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法 。 堆积是一个近似完全二叉树的结构 ， 并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点 。 7.1 算法描述
  • 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆 ， 此堆为初始的无序区；
  • 将堆顶元素R[1]与最后一个元素R[n]交换 ， 此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
  • 由于交换后新的堆顶R[1]可能违反堆的性质 ， 因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆 ， 然后再次将R[1]与无序区最后一个元素交换 ， 得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn) 。 不断重复此过程直到有序区的元素个数为n-1 ， 则整个排序过程完成 。
7.2 动图演示
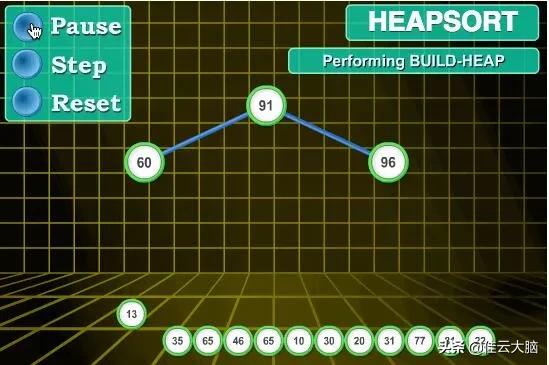十大经典排序算法（动图演示）文章插图
7.3 代码实现 1 function quickSort(arr, left, right) { 2varlen = arr.length, 3partitionIndex, 4left = typeofleft != 'number'? 0 : left, 5right = typeofright != 'number'? len - 1 : right; 67if(left < right) { 8partitionIndex = partition(arr, left, right); 9quickSort(arr, left, partitionIndex-1);10quickSort(arr, partitionIndex+1, right);11}12returnarr;13 }1415 function partition(arr, left ,right) {// 分区操作16varpivot = left,// 设定基准值（pivot）17index = pivot + 1;18for(vari = index; i <= right; i++) {19if(arr[i] < arr[pivot]) {20swap(arr, i, index);21index++;22}23}24swap(arr, pivot, index - 1);25returnindex-1;26 }2728 function swap(arr, i, j) {29vartemp = arr[i];30arr[i] = arr[j];31arr[j] = temp;32 }8、计数排序（Counting Sort）计数排序不是基于比较的排序算法 ， 其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中 。 作为一种线性时间复杂度的排序 ， 计数排序要求输入的数据必须是有确定范围的整数 。 8.1 算法描述
  • 找出待排序的数组中最大和最小的元素；
  • 统计数组中每个值为i的元素出现的次数 ， 存入数组C的第i项；
  • 对所有的计数累加（从C中的第一个元素开始 ， 每一项和前一项相加）；
  • 反向填充目标数组：将每个元素i放在新数组的第C(i)项 ， 每放一个元素就将C(i)减去1 。
8.2 动图演示8.3 代码实现【十大经典排序算法（动图演示）】 1 varlen;// 因为声明的多个函数都需要数据长度 ， 所以把len设置成为全局变量 23 function buildMaxHeap(arr) {// 建立大顶堆 4len = arr.length; 5for(vari = Math.floor(len/2); i >= 0; i--) { 6heapify(arr, i); 7} 8 } 910 function heapify(arr, i) {// 堆调整11varleft = 2 * i + 1,12right = 2 * i + 2,13largest = i;1415if(left



上一篇：SpringBoot整合JWT+Shiro

下一篇：厉害的何止华为！中兴突然“亮剑”，国产芯片再传捷报