缓存淘汰算法LRU和LFU 前言LRU算法和LFU算法是属于页面置换的

前言LRU算法和LFU算法是属于页面置换的一种算法，或者更通俗的说，就是缓存如何淘汰的一种策略。
我们通常在设计一个系统的时候，由于数据库的读取速度远小于内存的读取速度，所以为了加快读取速度，会将一部分数据放到内存中，称为缓存。
但是内存容量是有限的，当你要缓存的数据超出容量，就得有部分数据删除，这时候哪些数据删除，哪些数据保留，就是LRU算法和LFU算法要干的事。
什么是LRU算法LRU算法，全称Least recently used ，即最近最少使用。 LRU算法的思想是如果数据最近被访问过，那么将来被访问的概率也会很高。
根据这个思想，我们可以想到，实现LRU算法肯定会用到列表/链表，目的是保证有序；还有一个是用到哈希表，这是因为缓存经常是key-value键值对的形式。
比较简单的做法是使用列表+哈希表，但是这种方式查询和插入的时间复杂度都是O(n) ，还有一种做法是使用双向链表+哈希表，查询和插入的时间复杂度都是O(1) ，但是耗费的空间资源比较多。
列表+哈希表的实现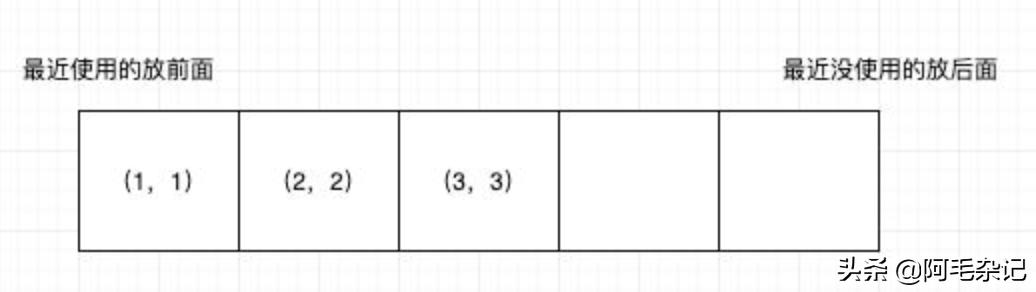
文章插图
如上图，假设我们使用头插法，即最近访问的元素放在最前面，最晚的元素放在最后面，则实现LRU算法的步骤如下：

1.初始化一个空列表，如上图，其容器为5 。
2.当执行查找（GET）操作时，需要遍历整个列表，找到key相同的元素，时间复杂度为O(n)
3.当执行插入（PUT）操作时，有三种情况：
3.1 遍历列表，如果元素的key存在，更新value的值，并把这个元素放到列表的最前面，从而保证最后面的元素是最晚访问的。
3.2 遍历列表，如果元素的key不存在，且列表的容量未满，则把这个元素放到列表的最前面
3.3 遍历列表，如果元素的key不存在，且列表的容量已满，删除最后的元素，并把新元素放到最前面

双向链表+哈希表的实现这应该是面试比较常考的点，面试官可能会问你，如果实现一个时间复杂度为O(1)的LRU缓存？
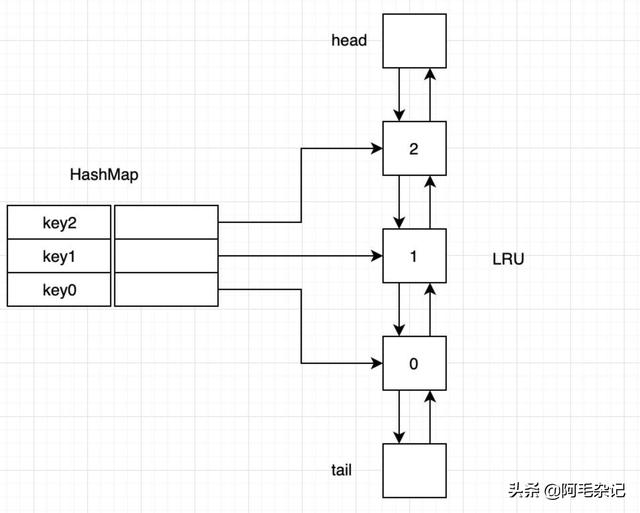
这种实现的结构如下：

文章插图
上述LRUCache的m其实就是上图左边的HashMap ，它的目的是为了实现查找的时间复杂度为O(1) 。
如果没有这个m ，则查找元素的时候，需要遍历双向链表，时间复杂度为O(n) 。
而使用双向链表的原因主要是为了实现节点插入/删除的时间复杂度为O(1) 。
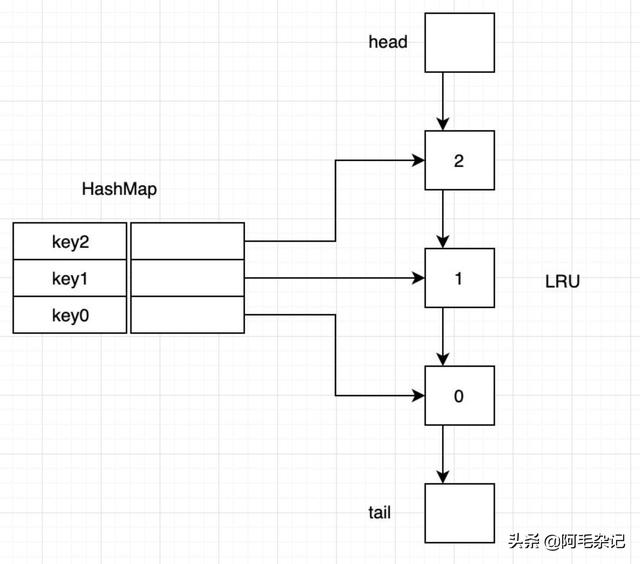
那使用单链表不行吗？

文章插图
如上，使用单链表的话，可以实现头部快速插入新节点，尾部快速删除旧节点，时间复杂度都是O(1) 。
但是对于中间节点，比如我需要节点1的值由2更新为4 ，这时候除了更新值，还需要将其移动到最前面，而对于单链表，它只知道下一个元素，并不知道上一个元素，为了得到上一个元素，它必须遍历一次链表才知道，时间复杂度为O(n) ，这就是为什么要用双向链表的原因。
关于这种方式的源码实现，可以查看Leetcode LRU双向链表实现
什么是LFU算法LFU算法，全称Least frequently used ，即最不经常使用。 LFU算法的思想是一定时期内被访问次数最少的节点，在将来被访问到的几率也是最小的。
由此可以看到， LFU强调的是访问次数，而LRU强调的是访问时间。
LFU有两种实现方式，一是哈希表+平衡二叉树，二是双哈希表，下面以双哈希表为例，说明LFU具体的步骤：
双哈希表的实现双哈希表的实现如下图：