「基础」奇异值分解的原理与应用选自machinelearningmastery

文章插图
选自machinelearningmastery ，作者：Jason Brownlee
本文转自机器之心（nearhuman2014）
矩阵分解在机器学习应用中的重要性无需多言。本文对适用范围很广的奇异值分解方法进行了介绍，并通过代码演示说明了其工作方式、计算方法及其常见的几种基础应用。
矩阵分解也叫矩阵因子分解，涉及到用给定矩阵的组成元素描述该矩阵。
奇异值分解（SVD）可能是最著名和使用最广泛的矩阵分解方法。所有矩阵都有一种 SVD 方法，这使得其比特征分解（eigendecomposition）等其它方法更加稳定。因此，这种方法在很多应用中都有应用，包括压缩、去噪、数据压缩。
在这份教程中，你将了解用于将矩阵分解成其组成元素的奇异值分解方法。
在完成本教程后，你将了解：

奇异值分解是什么以及涉及什么
如何计算 SVD 以及如何根据 SVD 元素重建矩形和方形矩阵
如何使用 SVD 计算伪逆和执行降维

那就开始吧！
教程概览
本教程分为 5 部分，依次为：
1. 奇异值分解
2. 计算奇异值分解
3. 根据 SVD 重建矩阵
4. 用于伪逆的 SVD
5. 用于降维的 SVD
奇异值分解
奇异值分解（SVD）是一种用于将矩阵归约成其组成部分的矩阵分解方法，以使后面的某些矩阵计算更简单。
为了说明简单，我们将关注用于实数值矩阵的 SVD ，而会忽略复数矩阵的情况。

文章插图
其中 A 是我们希望分解的 n×m 的实矩阵， U 是一个 m×m 矩阵， Sigma（通常用大写的希腊字母 ∑表示）是一个 m×n 的对角矩阵， V^T 是一个 n×n 矩阵的转置，其中 T 是上标。奇异值分解是线性代数的一个亮点。
——《Introduction to Linear Algebra》第五版， 2016 年，第 371 页
Sigma 矩阵中的对角值被称为原始矩阵 A 的奇异值。 U 矩阵的列被称为 A 的左奇异向量， V 的列被称为 A 的右奇异向量。
SVD 是通过迭代式的数值方法计算的。我不会详细深入这些方法的细节。每一个矩形矩阵都有一个奇异值分解，尽管所得到的矩阵可能包含复数值以及浮点算术的局限性可能会导致某些矩阵无法简单利落地完成分解。
奇异值分解（SVD）提供了另一种将矩阵分解成奇异向量和奇异值的方式。 SVD 让我们可以发现某些与特征分解同种类型的信息。但是， SVD 有更广的适用性。
——《Deep Learning》， 2016 年，第 44-45
SVD 在矩阵求逆等其它矩阵运算的计算有广泛的应用，但也可用作机器学习中的数据归约方法。 SVD 也可用在最小二乘线性回归、图像压缩和数据去噪中。
奇异值分解（SVD）在统计学、机器学习和计算机科学领域有很多应用。将 SVD 应用于矩阵就像是使用 X 射线进行透视……
——《No Bullshit Guide To Linear Algebra》， 2017 年，第 297 页
计算奇异值分解
SVD 可以通过调用 svd 函数进行计算。
该函数在处理矩阵后会返回 U、Sigma 和 V^T 元素。 Sigma 对角矩阵是按奇异值向量的形式返回的。 V 矩阵是以转置后的形式返回的，比如 V.T.
下面的示例定义了一个 3×2 矩阵并计算了奇异值分解。

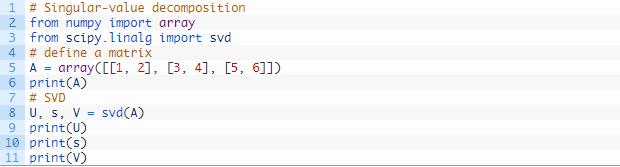文章插图
运行这个示例，首先会显示定义的 3×2 矩阵，然后会显示分解计算得到的 3×3 的 U 矩阵、2 个元素的 Sigma 向量和 2×3 的 V^T 矩阵元素。