数学|一道高难度印度数学竞赛题：解根式方程，正确率不到5% 数学

文章图片

文章图片

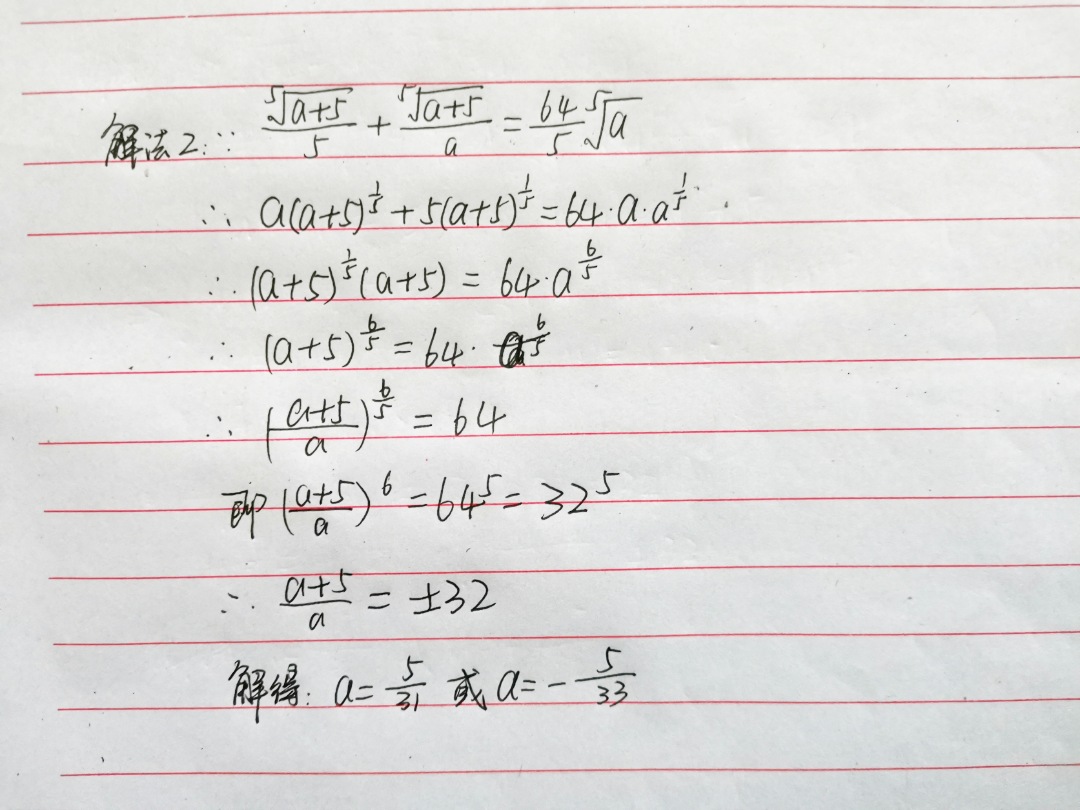
文章图片
初中阶段已经学习平方根、立方根等数字的简单开方运算，然后扩展到了二次根式等知识。对于不少学生来说，开方运算的难度比较大，特别是二次根式等内容。今天和大家分享一道高难度的印度初中数学竞赛题：解根式方程，据说当时的正确率不到5% 。
下面我们一起来看一下这道竞赛题。
这道题是一个五次根式的方程，不少考生看到这个方程心里多少有一些畏惧感。毕竟如果是国内，初中可没有学习太复杂的根式的计算，也没有学习分数指数幂的计算，所以这道题让不少学生觉得很难找到突破口，那么该怎么办呢？
既然没有学过分数指数幂以及开五次方的计算，那么我们就先想办法把开五次方变成常见的整数指数幂的计算，所以可以考虑使用换元法。
比如我们可以设5√(a+5)=m ， 5√a=n ，则a=n^5 ，且m^5-n^5=5 ，再联合题目给出的方程即可组成一个关于m、n的二元方程组，而且这个二元方程组不需要把m、n完全解出来，只需要解出n^5的值即可。过程如下：
在上面的计算中，需要注意对64^5的处理，要将其变成某个数的6次方，即32^6 ，这样才方便后续的计算。另外，在开六次方的时候，因为开的是偶数次方，所以需要注意数值的正负，并且要代入题干进行检验。本题中，开方后的正负数都满足要求，所以有正负两个值。
当然，有网友表示这是一道竞赛题，用到一点书本以外的知识也是无可厚非的，所以直接用分数指数幂的运算法则计算即可。那么我们先来看一下分数指数幂的运算。
【数学|一道高难度印度数学竞赛题：解根式方程，正确率不到5%】首先，明确一点，根式可以写成分数指数幂的形式，比如开平方就是二分之一次方，开立方就是三分之一次方，开五次方就是五分之一次方。
其次，不管指数是整数还是分数，其运算法则都和整数是一样的。
有了上面的知识准备，那么这道题也可以不用换元法直接求解。为了方便计算，先将根号写成分数指数幂的形式，再按照分数指数幂的运算法则进行计算即可。
总结：本题的难点主要有以下两点：
第一、如果是采用换元法，最后得到的方程次数高，不少考生尝试一下后就放弃了。如果不换元，那么又需要用到分数指数幂的运算，而这一点在初中阶段并没有系统学习；
第二、在开六次方的时候，不少学生直接忽略了负数这个值，导致漏解。
总的来说，这道题的难度很大，考生的正确率也不高。你觉得这道难吗？