数学|这道竞赛题求四边形面积，多数人不知所措，面积与比例结合是关键数学

朋友们，大家好！今天是2020年10月5日星期一，数学世界将继续为大家分享小学高年级的数学竞赛题。大家知道，数学世界最近发的文章都是能力提高类型的数学题，但是笔者看到有不少读者留言，嫌题目简单了。对此，我就纳闷：难道你们都是学霸吗？
有些人可能是用了初中知识来做小学数学题吧，所以强调一下，小学数学题只能用小学阶段的知识解答！言归正传，今天我们讲解一道有关求四边形面积的数学题，此题有较大的难度，对于绝大多数学生来说是很难做出来的，若能正确解答肯定是尖子生。要解决这道题，必须具备较强的图形转换思维。
虽然此题属于比较难的数学题，但是学生依然能够完全用小学阶段所学知识解答出来。数学世界在此分享这些有趣的数学题，目的是希望能够激发学生学习数学的兴趣，并且能够给大家的学习提供一些帮助！
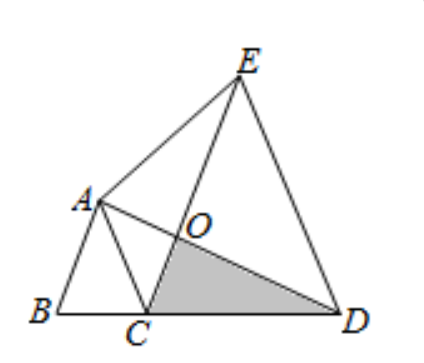
例题：（小学数学竞赛题）如图所示，已知AB和CE平行， AC和DE平行， AB=AC=5厘米， CE=DE=10厘米，若三角形COD的面积为10平方厘米，求四边形ABDE的面积是多少平方厘米？
【数学|这道竞赛题求四边形面积，多数人不知所措，面积与比例结合是关键】这道题要求的是四边形的面积，显然只能通过求三角形的面积来解决，但是图形中没有给出任何一条高，只能想办法寻找相关图形面积之间的关系。对于学生来说，要解决这样的数学题，需要有较强的图形识别能力。接下来，数学世界就与大家一起来完成这道例题吧！
分析：仔细观察图形，由题意，根据“AB和CE平行， AC和DE平行”可以推出三角形面积之比与边的比之间的关系，由此求出OC/OE的比，进而求出各个三角形的面积，按此解答即可解决问题。下面，我们就来解答此题吧！
解答：因为AC和DE平行，
所以△ACE和△ACD等底等高，
于是S△ACE=S△ACD ，
同时减去空白△ACO ，
可得S△AOE=S△COD ，
根据等高三角形面积与底的关系，得
OC/CE=S△COD/S△CDE ，
OE/CE=S△AOE/S△EAC=S△COD/S△EAC ，
所以OC/OE=S△EAC/S△CDE ，
因为三角形EAC在边AC上的高和三角形CDE在边DE上的高相等，
所以OC/OE=S△EAC/S△CDE=AC/DE=5/10=1/2 ，
因为△COD和△CDE等高，
所以S△COD/S△CDE=OC/OE=1/2 ，
所以S△DOE=2S△COD=20平方厘米，
同理S△AOC/S△AOE=OC/OE=1/2 ，
所以S△AOC=1/2S△AOE=1/2S△COD=5平方厘米，
所以S△ACE=S△AOC+S△AOE=15平方厘米，
因为AB和CE平行，
所以三角形ABC的边AB上的高和三角形ACE的边CE上的高相等，
所以S△ABC/S△ACE=AB/CE=1/2 ，
即S△ABC=1/2S△ACE=1/2×15=7.5平方厘米，
所以四边形ABCDE的面积为
S△ABC+S△ACE+S△COD+S△DOE
=7.5+15+10+20=52.5（平方厘米）
答：四边形ABDE的面积是52.5平方厘米。
（完毕）
这道题主要考查了等底或等高三角形面积的关系，以及面积与比例的结合。解答此题的关键是：灵活运用三角形面积之比与边的比之间的关系。温馨提示：朋友们如果有不明白之处或者有更好的解题方法，欢迎大家留言讨论。