##最近很火的“硬币悖论”，怎么就扯上了摆线、圆心运动、圆周长公式？

文章图片

文章图片

最近一个硬币转动的视频在某平台上又掀起了轩然大波，评论区的各种回复五花八门，数不胜数，而且是越讨论越复杂。还有很多科普视频甚至于将圆周长公式、摆线、圆心运动、齿轮效应、直线上点的数量的无限性等概念都搬了出来对问题进行解释，其实，真用得着这么多毫无关系的概念吗？毫无疑问，这些科普内容明摆着将简单问题复杂化了，失去了科普（科学）所必须具有的简明化精神。

问题是这样的，两枚硬币紧挨在一起，固定好其中一枚硬币，让另一枚硬币无滑动地围绕固定好的硬币转动一圈，问转动的硬币转过（自转）了几圈？
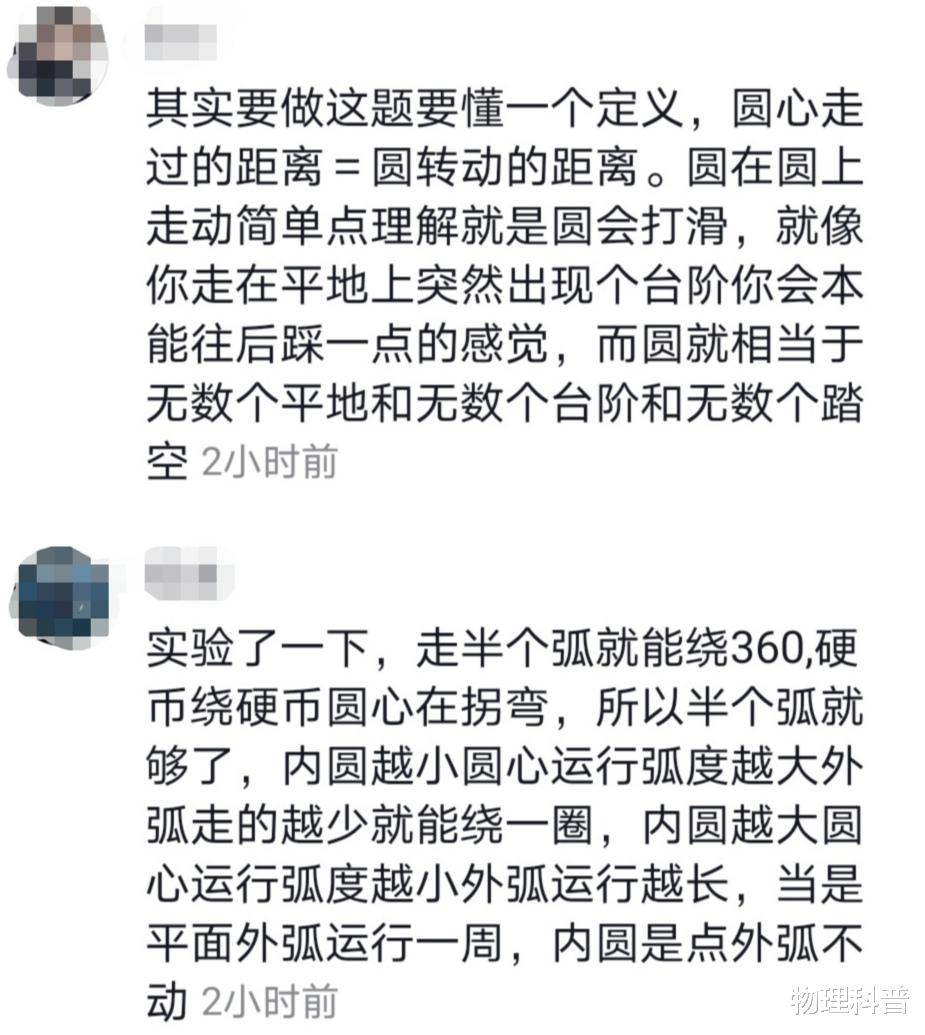
先来看看评论区的回复！那些将问题复杂化的科普内容就不列举了。
“一圈，不要跟我说什么外面的圈更大，硬币之间无滑动的话外面那圈就是有滑动的运动。 ”“两圈，外面的硬币上取一点是在做摆线运动。 ”“一圈，一样大。 ”“月亮绕地球一周，月球自己就转了一圈。 ”“也是一圈啊，齿轮效应啊，运动是相对的。 ”
很多人质疑原视频中提问题时，并没有讲清楚圈的定义。其实原问题中圈的定义很清楚，意思明显是在问，转动的硬币自转的圈数是几圈。我们现在来看看，以最直接最简明的方式分析清楚了这个问题后，圆周长公式、摆线、圆心运动、齿轮效应、直线上点的数量的无限性这些概念，将如何被痛快地抛弃掉？
因为是无滑动转动，因此转动硬币围绕固定好的硬币转动一圈，其接触点在转动硬币上必然经过一个完整的硬币周长，因此接触点在转动硬币上的变动会使转动硬币自转一圈。再假设原先无滑动转动的硬币，以一个固定的接触点纯滑动式地围绕固定好的硬币转动一圈，这又将使硬币自转一圈。这时可看出来，硬币无滑动围绕一圈的实际效果是，硬币在每个接触点上无滑动转动时，固定好的硬币上接触点在转动的基础上，转动的硬币上接触点在反方向转动，因此结果是转动硬币两个同向自转的叠加，答案是两圈。
【##最近很火的“硬币悖论”，怎么就扯上了摆线、圆心运动、圆周长公式？】好了，一句话就阐明得清清楚楚的问题，明明可以用两个接触点反向转动的叠加来解决的问题，非要扯出来一些毫无关系的概念绕着圈子解释，将问题复杂化，这种精神已经与科普的意义背道而驰了。