「火星」经常看到第一、第二、第三宇宙速度，为何很少提到第四宇宙速度？科学家|核战争

文章图片

文章图片

文章图片

文章图片

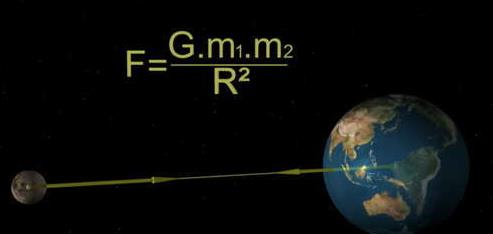
在17世纪80年代，伟大的物理学家年顿发现了万有引力定律，指出任何有质量的物体之间都存在着万有引力，使之具有相互吸引的趋势，这个引力的数值与两者的质量乘积成正比，与它们之间距离的平方值成反比。万有引力的提出，揭示了宇宙中所有物质的基本运动规律，特别对于宇宙中的大质量天体来说，对其运行特点以及轨道特征的研究具有重要意义，从而奠定了宇宙天体力学的基础。
宇宙中的所有天体，在其形成演化的过程中，其吸聚的众多星际气体和尘埃物质本身具有的角动量，最后全部转化为天体本身以及围绕天体运行天体的角动量，使天体呈现周期性的自转，同时围绕着天体运行的其它物质也以一定的周期围绕其公转。而从围绕天体运行的物体来看，其在围绕大质量天体公转的过程中，所受到天体的万有引力形成的重力加速度，正好与公转时的向心加速度相同，于是该物体就可以围绕着该天体作匀速的圆周运动，距离天体越近，则所需要的向心加速度就越大，物体要保持稳定的公转，其水平方向上的运动速度就要越快。
在牛顿发现万有引力定律之后， Bonnet将一个天体围绕另外一个天体公转的速度问题，表述为在许多等效的独立力场作用下，所有分力场共同推动产生的等效综合加速度起到的效果，其数值等于各个独立力场所形成的等效速度平方和的算术平方根。那么，对处于匀速圆周运动的天体来说，表现出来的分力场效果将最终集中在运动轨迹的切向方向和法向方向上，其中切向方向上的速度为线速度，法向方向上的速度为引力源对其的拉力效果。当物体围绕天体公转的线速度不够时，即沿着切向方向移动的距离，达不到因物体移动所“拉开”的与天体之间的空间距离时，那么这个由万有引力引发的拉力，将会使物体的运动轨迹不断向引力源中心“坠落” 。
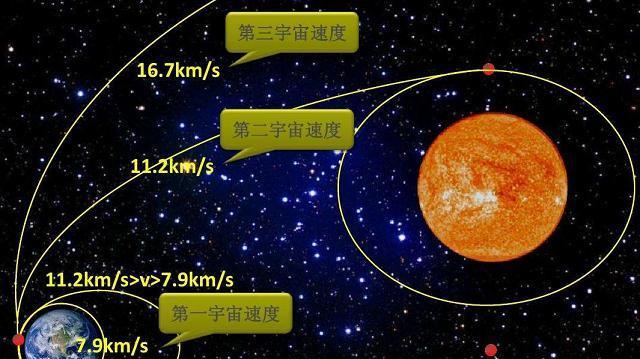
基于上述原理，科学家们在判断一个物体能否围绕该天体正常运行时，引入了第一、第二和第三宇宙速度的概念，它们分别表示可以环绕地球运行、脱离地球引力束缚、脱离太阳系引力束缚3种条件下的最低水平运行速度。这3个最低速度的推导，其实应用的都是牛顿万有引力公式和向心力公式，先找到物体能够围绕引力源运行的临界速度，这个速度值为V＝Sqrt(GM/r) ，其中G为引力常数、M为引力源质量、r为物体与引力源中心的距离。
对于第一宇宙速度来说，就是可以达到物体围绕地球作匀速圆周运行的最小速度，通过代入数值计算，可以得出V1＝7.9公里每秒，而实际我们发射卫星、航天器时，由于大气层的存在，不可能贴近地面绕行，必须远离一定的高度，一般需要在120公里以上，因此考虑到这个因素，第一宇宙的数值会有所下降，大约为7.8公里每秒。
对于第二宇宙速度来说，因为它是需要脱离引力源引力束缚的最小速度，因此在判断这个临界值时，考虑的是物体的动能刚好等于物体的重力势能，即1/2*m*V2^2=G*M*m/r ，然后推导出V2=Sqrt(2GM/r) ，可以看出，第二宇宙速度的值是第一宇宙速度的根号2倍。当以地球为引力源时，那么将相关数值代入，可以计算出V2＝11.2公里每秒。