蚌埠@初中数学备考必刷038-原来正方形夹半角模型还可这么考!
文章图片
文章图片
正方形是八年级下学期的教学重点也是考试重点 , 期中和期末考试里都经常出现 , 而且往往会是压轴题 。 提前研究好正方形 , 说不定你可以轻松搞定压轴题 , 拿个高分 。
今天给大家分享的是武汉硚口区2020年八下数学期中考试的压轴题 , 考查的是正方形夹半角模型 , 第一问送分题 , 后面的两个问题就考查变通能力了 。
我们先来看看题目:
武汉硚口区2020八下期中考试压轴题.
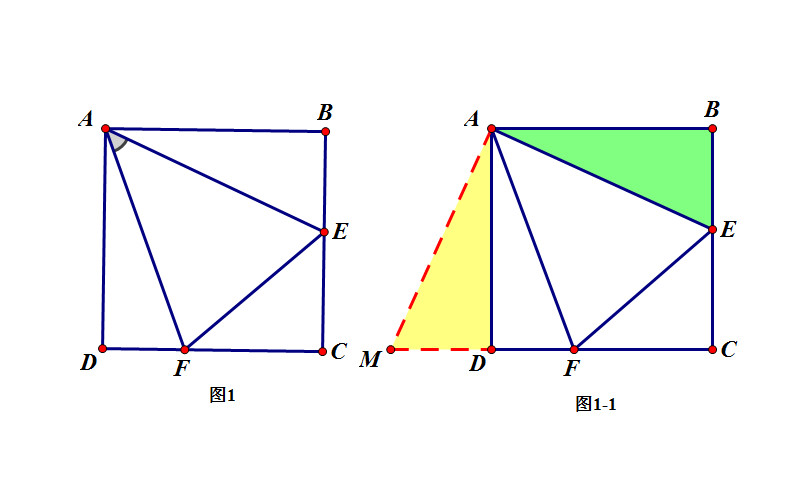
(1)如图1 , 正方形ABCD , ∠EAF=45° , E在BC上 , F在CD上 , 求证BE+DF=EF
(2)如图2 , 正方形ABCDPA与PB交于P点 , 角APB=45° , CH=3 , GH=1求AG.
(3)如图3 , 在长方形ABCD中∠EAF=45° , E在BC上 , F在CD上 , DF:AD:AB=1:2:4求BE和CE的数量关系 。
(1)问很简单 , 这是一个典型的正方形夹半角模型 。
证明:如图1-1延长CD至M , 使MD=BE连接AM.
在△ABE和△ADM中:AB=AD∠ABE=∠ADMBE=DM
∴△ABE△ADM
∴∠MAD=∠EAB∠MAD+∠DAF=45° , AM=AE
在△AMF和△AEF中:AM=AE∠MAF=∠EAF=45° , AF=AF
∴△AMF△AEF
∴EF=MF=MD+DF=BE+DF
(2)分析与解答:根据正方形夹半角模型来看 , 至少需要具备以下三个典型特征:
正方形 , 45°角 , 45°角的顶点与正方形的某个顶点重合
【蚌埠@初中数学备考必刷038-原来正方形夹半角模型还可这么考!】此题中已给出了正方形 , 但是另外两个特征不明显 , 我么就需要做出辅助线来满足45°角和45°角的顶点与正方形的某个顶点重合的特征 。
题目已经给出了∠APB=45° , 只需作AM⊥PB交BP于N , 交BC于M , 这样就有完整的正方形夹半角模型呈现出来 。 并且还具备正方形中的十字架模型特征:AM⊥BH.
简解:作AM⊥BP分别交BP于N , 交BC于M , 连GM 。
易证:△ABM△BCH(ASA)所以BM=CH=3.
设DG=m根据第一问结论可知GM=DG+BM=m+3.
CM=BC-BM=DC-BM=m+1+3-3=m+1
在Rt△CMG中:
(GM^2)=(MC^2)+(GC^2)解:m=2.
AD=DC=m+4=6DG=2易求AG=2√(10).
(3)分析与解答:根据正方形夹半角模型来看 , 至少需要具备以下三个典型特征:正方形 , 45°角 , 45°角的顶点与正方形的某个顶点重合 。
此题中已给出了45°角 , 并且45°角的顶点与长方形的顶点A重合 , 那我们就构造正方形 。
构造正方形有两种方式:
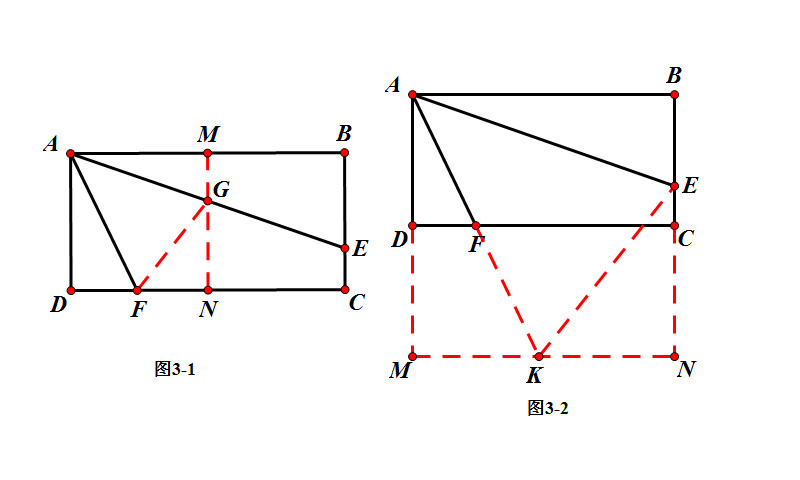
法1:如图3-1 , 根据AD:AB=2:4取AB中点M , 作MN垂直DC则四边形ADNM是正方形MN交AE于G连GF.
法2:如图3-2 , 根据AD:AB=2:4分别倍长AD和BC至MN.连MN则四边形AMNB是正方形 。 EK , 延长AF交MN于K.
法3:12345模型秒解:DF:AD=1:2则BE:AB=1:3
- 初中数学@初中数学三角形倒角模型专题“8字模型”(含经典练习附答案)
- 数学■小学数学1-6年级基础复习资料,融会贯通后,成绩稳步提高
- 「临床医学」2020广州一模理科数学试题及答案
- 「数学」整理小升初六年级数学总复习资料,请收藏
- 『高中数学』高中数学:选修2-3知识点清单,内容不多,收藏打印下来背记
- 蚌埠检察市检察院参加创建全国文明城市“一场一巷一小区”包保点位检查督导工作
- #数学#小学生数学题目难倒985毕业家长,直言被题目绕晕,网友:不会做
- 「数学」一道一年级数学题,家长想了两个小时,硬是不知道孩子错在哪
- 高中数学@高中数学精选好题400道,吃透高考答题准确率提升一大截!含答案
- #数学#一道一年级数学题,全班59个学生\全军覆没\,家长:真不怪孩子
