#黎曼猜想#如何让全球银行都破产，你只需要攻克黎曼猜想破产

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

有人问过希尔伯特一个问题，说：“如果你沉睡了几百年，然后醒过来，你想干什么？”希尔伯特说， “我想问问有人把黎曼猜想证出来了吗？我太想知道了” 。

如何让全球银行破产，是全球经济大萧条，还是战争摧毁了文明？都不是，你只需要破解黎曼猜想。
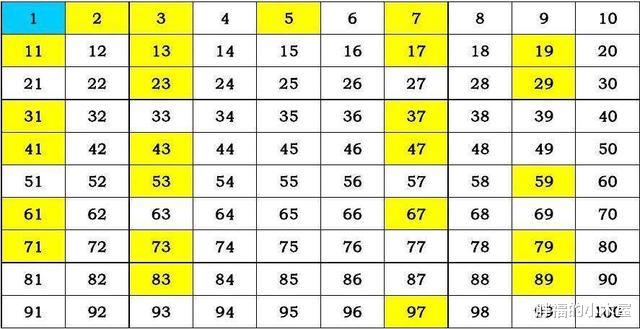
黎曼猜想是什么简单来说，黎曼猜想究竟讲了什么呢？就是一个寻找质数的方法。
什么是质数呢？我们应该在初中就学习过，就是指那些只能被1和自己所整除的数，如2、3、5、7、11等等。质数的研究属于数论的范畴。
早在古希腊时期，欧几里得的《几何原本》中就有对质数的研究。欧几里得采用反证法证明了质数有无穷个，但是质数究竟有什么分布规律呢？欧几里得并没有找到。
至此之后，数学家们都费劲心思想要找寻质数分布的规律， 1859年，黎曼发表了《论小于已知数的质数个数》论文探究质数分布的奥秘，这篇只有短短八页的论文就是黎曼猜想的“诞生地” 。
论文手稿
在这篇论文中，黎曼通过研究，发现质数出现的频率的规律，提出了黎曼Zeta函数，黎曼Zeta函数是一个无穷级数的求和。
Zeta函数
黎曼对解析延拓后的Zeta函数证明了其具有两类零点。其中一类是某个三角sin函数的周期零点，这被称为平凡零点；另一类是Zeta函数自身的零点，被称为非平凡零点。针对非平凡零点，黎曼提出了三个命题。
第一个命题，黎曼指出了非平凡零点的个数，且十分肯定其分布在实部大于0但是小于1的带状区域上。
第二个命题，黎曼提出所有非平凡零点都几乎全部位于实部等于1/2的直线上。
而第三个命题就是重头戏了：很可能所有非平凡零点都全部位于实部等于1/2的直线上。
这第一个命题，黎曼表示太简单了，压根不需要证明，然而直到86年之后，第一个命题才由德国数学家蒙戈尔特在给出了完整的证明。
而至于第二个命题，黎曼声称自己已经证明，但是证明过程还需要简化，然而因为饱受病痛折磨，黎曼39岁就英年早逝，去世之后，他的手稿被管家付之一炬，自此黎曼的证明过程就彻底消失人间。
1932年。一位德国数学家Siegel整理黎曼仅存的手稿，让黎曼当时演算零点所用的公式重见天日，这个公式被命名为Riemann-Siegel公式。