阿基米德：高考数学命题的一个藏宝库----阿基米德三角形( 二 ) 数学

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片
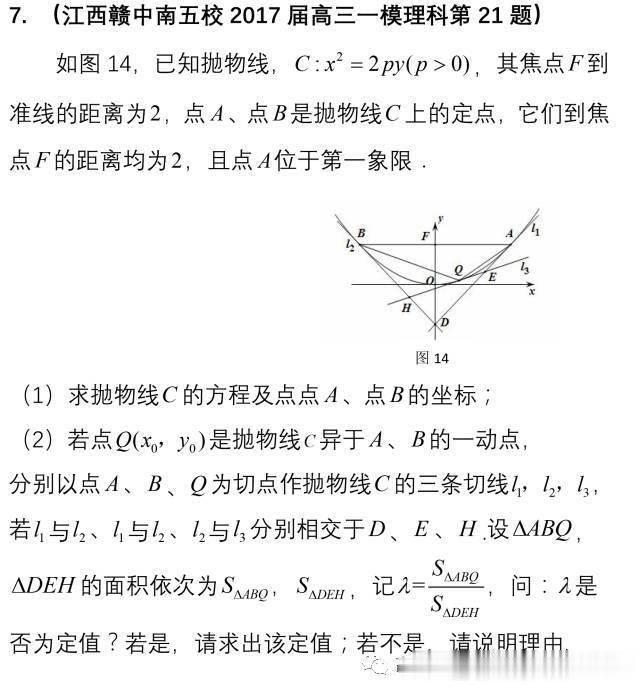
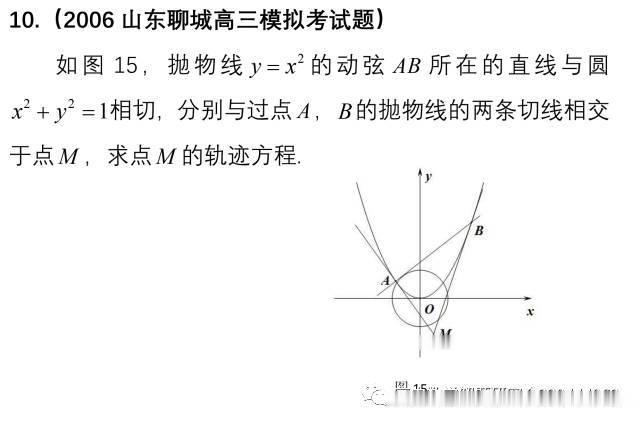
本文以两个定理及推论的形式归纳出有关阿基米德三角形中点、线、面积的8条常用性质，从17个角度归纳出由阿基米德三角形衍生的五种类型的高考试题，探究同宗同源问题的命题规律和解题规律，文末链接了若干源于阿基米德三角形的相关模拟题。
1
阿基米德三角形的性质
抛物线的弦与过弦的端点的两条切线所围的三角形，称为阿基米德三角形。
阿基米德三角形的得名，是因为阿基米德本人最早利用逼近的思想证明了如下结论：
抛物线的弦与抛物线所围成的封闭图形的面积，等于抛物线的弦与过弦的端点的两条切线所围的三角形面积的三分之二（见本文推论2（2））。
在普通高中课程标准实验教科书·数学选修3-1（A版）《数学史选讲》(人民教育出版社2007年1月第2版)第21页中，有这个结论的另外一种变式叙述。
阿基米德(Archimedes ，公元前287～公元前212) ，是古希腊伟大的物理学家、数学家、天文学家和机械发明家，他的数学贡献史无前例，享有“数学之神”的称号。他在两千二百多年前使用睿智的“平衡法” ，也就是杠杆原理研究抛物线的求积问题，实际上就是近代积分的思想。
为了后文的应用方便，我们先对阿基米德角形相关性质做些归纳。
定理1
证明
推论1
证明
定理2
证明
推论2
证明
2
阿基米德三角形的应用
自公元前3世纪至今，历经了两千多年的风霜雨雪，阿基米德三角形尤如一颗闪烁的明珠，以其深刻的背景，丰富的内涵产生出了无穷的魅力，在数学发展的历史长河中不断地闪烁出真理的光辉。这个两千多年的古老图形，如同一个题库，里面蕴藏着各级各类考试命题高考素材。
由阿基米德三角形衍生出的高考题，主要有以下五种类型。
2.1
线段长度问题
角度1
角度2
从角度1和角度2切入，可编拟：
角度3
角度4
从角度3和角度4切入，可编拟：
2.2
轨迹问题
角度5
角度6
从角度4和角度5切入，可编拟：
角度7
角度8
角度9
从角度7 ，角度8和角度9切入，可编拟：
2.3
切线问题
角度10
角度11
从角度10和角度11切入，取P=1/2 ，可编拟：
角度12
从角度12切入，可编拟：
2.4
最值问题
角度13
角度14
从角度13和角度14切入，可编拟：