凝聚态|对称破缺——凝聚态中的物理美还原论|对称性破

图1：凝聚态大师朗道和安德森
撰文 | 张天蓉
责编 | 宁茜
巴丁（John Bardeen ， 1908 – 1991）所获的两次诺奖都与凝聚态研究有关。凝聚态以量子理论为基础，在量子场论建立之后，理论物理朝两个不同的方向发展：粒子物理（particle physics）和凝聚态物理（condensed matter physics）。公众的眼光大多数投向传统的、以还原论思想为指导的高能粒子物理，以为那才是物理的正统方向。
然而实际上，当今的物理学家中，很大一部分是在做凝聚态物理的相关研究，包括理论和实验两个方面。凝聚态物理的理论部分，与粒子物理理论有许多相通之处。近百年来从固体到凝聚态的研究，在实用上促进了信息技术蓬勃发展，带给人们一次又一次的惊喜，典型范例是晶体管和超导。凝聚态物理在理论上独树一帜：凝聚态研究遵循的层展论，对科学思想、科学哲学等方面作出了重大贡献；凝聚态有关对称破缺的思想，被用于粒子物理中获取质量的希格斯机制。
朗道的相变理论
前苏联知名物理学家列夫·朗道（Lev Landau ， 1908-1968）是物理界的一位大师级人物，在理论物理多个领域中都有重大贡献。在中国学术界的心目中，朗道和费曼一样，是一位“学术卓著、特立独行”的传奇性人物。费曼因他的数本自传式读物而广为人知，朗道则以其一系列大厚本的经典物理教材而享誉学界。有关朗道的故事，如此一篇文章是写不完道不尽的，请见参考资料[1] 。

图2：年轻的朗道与玻尔、海森堡、泡利、伽莫夫等在一起
朗道的费米液体（Fermi Liquid）及相变（Phase Transition）等理论，奠定了整个凝聚态物理的基础。费米液体理论，让我们可以在处理多粒子的凝聚态物理中继续使用单粒子图像。此外，朗道提出的相变理论与对称性破缺理论相关，让我们能够用序参量来描述凝聚态系统的宏观态，使用对称性来给不同物相进行分类。
一般的物质有固、液、气三态，这是初中物理告诉我们的知识。后来，现代物理的研究结果，将“物质三态”的概念扩大——有了等离子态、波色-爱因斯坦凝聚态、液晶态等等，见图3 。再后来，又扩展细分到物质的许多种不同的“相” 。物质相之间的互相转换被称之为“相变” 。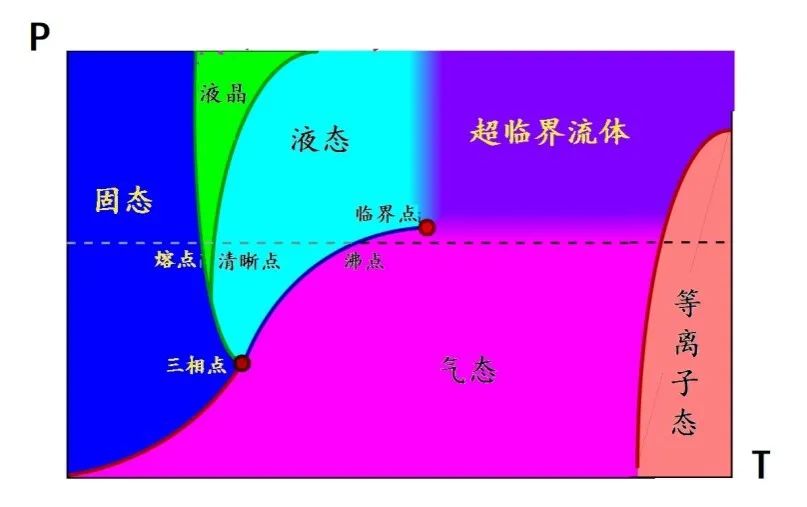

图3：相变图（包括液晶和等离子体）
固、液、气三相的变化，相应地伴随着体积的变化和热量的释放（或吸收）。这一类转换叫做“一级相变” ，它们的数学意义是说：在相变发生点，热力学中的参量（比如化学势）不变化，而它的一阶导数（体积等）有变化。后来，实验中不断观察到的物质相及相变的数目多了，一级相变的概念便被扩展到“二级”、“三级”……N级相变，分别用热力学量的N阶导数来区分。
这些N级相变，被统称为“连续相变” 。朗道对连续相变建立数学模型，提供了一个统一的描述[2] 。他认为连续相变的特征是物质的有序程度的改变，可以用序参数的变化来描述。或者更进一步，可以看成是物质结构对称性的改变。
根据物质的对称性及其破缺的方式来研究相和相变的方法被称为“朗道范式” 。也可以说由此方式才催生了凝聚态物理[3] 。物理学家们越来越认识到，分别单独地研究固体或液体，都远远满足不了实际情况的需要。特别是掺和了低温物理之后，固体物理的研究转向了对大量粒子构成的各种体系的研究。这些系统中的粒子具有很强的相互作用，在各种物理条件下，不仅仅表现为固态、液态、液晶态、等离子态，还有超流态、超导态、波色子凝聚态、费米子凝聚态……对这些千姿百态以及它们互相转换的研究，便构成了凝聚态物理。
【凝聚态|对称破缺——凝聚态中的物理美】安德森挑战还原论
研究凝聚态物理并做出开创性奠基的另一位大师，是美国物理学家菲利普·安德森（Philip Anderson ， 1923-2020）。
今年春天，安德森以97岁高龄不幸辞世，他在对称性破缺、高温超导等诸多领域都做出了重大贡献。当他在新泽西的贝尔实验室工作时，首先提出凝聚态中的局域态、扩展态的概念和理论，为此他和另一位美国物理学家约翰·范扶累克（John Hasbrouck van Vleck ， 1899-1980）及英国物理学家内维尔·莫特（Sir Nevill Francis Mott ， 1905-1996），分享了1977年的诺贝尔物理学奖。
除了对物理本身的杰出贡献之外， 1972年，安德森在《科学》杂志上发表的著名的“More is different”（《多则异》）的论文[4] ，针对一切归于最简单粒子的还原论（Reductionism），提出各种不同物质层次形成不同分支的层展论（Emergence），被认为是凝聚态物理的独立宣言，带给了整个科学界另一个认识这个世界的视角，表达了安德森对人类传统科学方法的挑战和超越。分页标题
传统的科研方法以还原论为主，古希腊的科学就是从“追本溯源” ，即“还原”开始的。所谓还原论，就是认为复杂系统可以化解为各部分的组合，并且，复杂体系的行为可以用其部分的行为来加以理解和描述。例如，物质由分子组成，分子由原子组成，原子又由更深一层的基本粒子组成，依次递推，构成了物质结构中越来越小的层次。还原论的方法便是逐层级地回答问题，期待深一层的结构能解释上一个层次所表现的性质。如此下去，科学演化的路线似乎归结为一条还原的路线，最后追溯到一个“终极问题” 。
然而，安德森提出不同的观点。他认为“多则异” ，还原并不能重构宇宙，部分行为不能完全解释整体行为。高层次物质的规律不一定是低层次规律的应用，并不是只有底层基本规律是基本的，每个层次皆要求全新的基本概念的构架，都有那一个层次的基础原理。也就是说，安德森教给我们不同于还原论的另一种认识这个世界的视角，即“层展论”（或称整体论）的观点。层展论既不属于还原论，也不反对还原论，而是与还原论互补，构成更为完整的科学方法。
安德森在他的《多则异》的文章中，以凝聚态中的对称破缺为例，说明层展论。
相变——对称和对称破缺
对称性的概念不难理解，在自然界及人工的建筑、艺术等领域，几何对称现象随处可见。固体中的晶格是一种空间状态重复的几何对称结构。如果将整个晶体移动一个晶格常数a ，结果仍然是原来的系统。换言之，晶格结构具有在空间平移a的变换下系统保持不变的对称性。所以，对称的意思就是系统在某种变换下保持状态不变。除了空间平移变换之外，还有空间旋转、空间反演等等其它种类的变换。除了在三维空间的各种变换之外，还有对于时间的平移或反演变换，以及其它抽象的或内禀性质的变换。各种变换对应于各种不同的对称性。
物理学中有一个诺特定理（Noether's theorem），由德国女数学家埃米·诺特（Emmy Noether ， 1882-1935）发现，它将物理中的守恒定律与对称性联系在一起[5] 。例如，能量守恒定律对应时间对称性；动量守恒对应空间平移对称；角动量守恒对应旋转对称性等等。我们在此不予详述，可见参考资料[6] 。
大千世界不仅有对称，也有不对称。观察我们周围的世界：人的左脸并不完全等同于右脸，大多数人的心脏长在左边，大多数的DNA分子是右旋的，地球并不是一个完全规则的球形……正是因为对称中有了这些不对称的元素，对称与不对称的和谐交汇，才创造了我们丰富多彩的世界。
即便是对称的情况，也有各种等级的高低之分。比如说，一个正三角形，和一个等腰三角形比较，正三角形应该更为对称一些；球面比椭球面具有更多的对称性。此外，物体状态的对称性也会变化，从低到高，或者从高到低。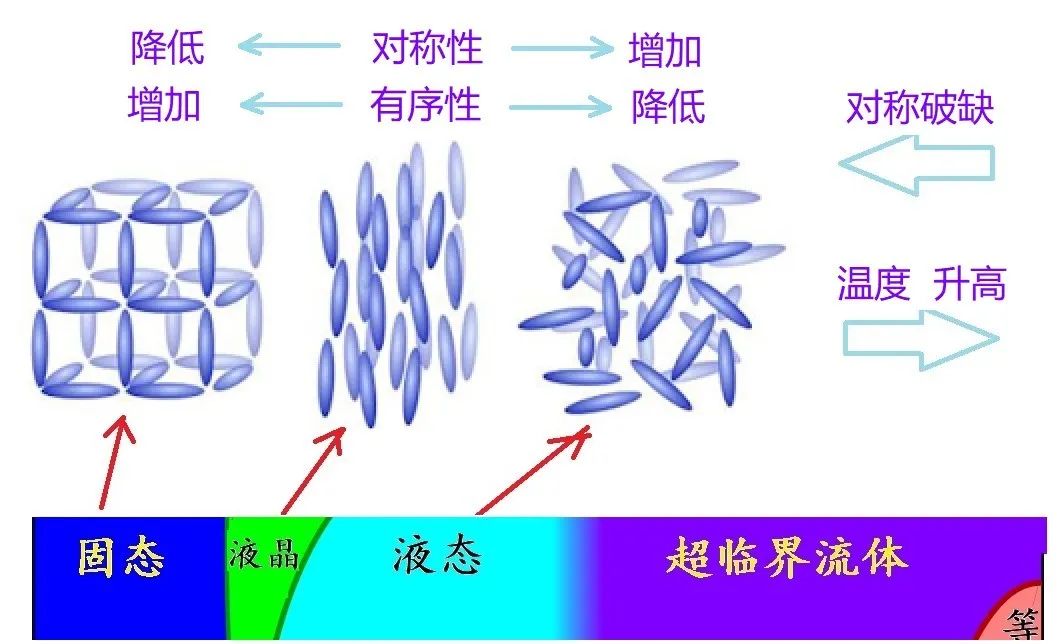

图4：相变和对称破缺
朗道将凝聚态物理中的相变与物质结构中对称性的变化联系在一起。他把从高对称到低的对称过程叫做“对称破缺” 。相应的，反过来的相变则意味着“对称恢复” 。然而，如何判断对称性的“高低”呢？特别需要提醒的是：有时候我们会将“对称性”与“有序性”等同起来，但事实上这两个概念的“高低”程度正好相反。越有序的结构，对称性反而越低。以下举个简单例子来说明。
图4上方所示的是“固态→液晶→液态”过程中物质分子结构的变化。这三者的对称性，到底孰高孰低呢？
固态中水分子有次序地排列起来，形成整齐漂亮的格子或图案（晶格）；在液晶中，三维晶格被破环了，成为一维晶体。之后，随着温度继续升高，一维的有序结构也被破坏而成为无序的液体：液态中的水分子做着随机而无规则的布朗运动（Brownian Motion）——没有固定的方向，没有固定的位置，处于完全无序的状态，在任何方向、任何点看起来都是一样的。而这正是我们所谓的对称性最“高”的状态，也就是说，液态的对称性很高，却无序。液晶和固态，相较液态而言，有序程度逐渐增加，对称性却逐步降低。
用数学的语言来描述的话，液态时，如果将空间坐标作任何平移变换，系统的性质都不会改变，表明对空间的高度对称。而当水结成冰之后，系统只在沿着某些空间方向，平移晶格常数a的整数倍的时候，才能保持不变。所以，物质从液态到固态，对称性降低，也就是破缺了，从连续的平移对称性减少成了离散的平移对称性。或叫做：固态破缺了液态的连续平移对称性，即晶体是液体的任意平移对称性破缺的产物。相比于液体，晶体的粒子密度出现了空间上的周期调制，因而更加有序，而从无到有的周期调制的变化，便可以表征物质从液体结晶为固体时的相变。
对称破缺（Symmetry Breaking）分为两大类：明显对称性破缺（Explicit Symmetry Breaking）和自发对称性破缺（Spontaneous Symmetry Breaking）。第一类“对称破缺”的原因是自然规律决定的，是因为某些物理系统本身就不具有某些物理规律对应的对称性，这类对称破缺的著名例子是李政道与杨振宁发现的“弱相互作用中宇称不守恒”（CP violation）。分页标题
第二类“自发对称破缺”是物理学家更感兴趣的。这种情况下，物理系统仍然遵循某种对称性，但物理系统更低的能量态（包括真空态）却不具有此种对称性。这种对称破缺的著名例子包括超导物理中的BCS理论，以及基本粒子标准模型中的希格斯机制（Higgs Mechanism）。
自发对称破缺
将“自发对称破缺”再表达得更清楚一些，就是说物理规律具有某种对称性，但是它的方程的某一个解，也就是物理系统实际上所处的某个状态，却不具有这种对称性。这样，我们看到的世界中一切现实情况，都是“自发对称破缺”后的某种特别情形。因此，它只能反映物理规律的一小部分侧面。图5中举了几个日常生活中的例子来说明对称性的“破缺” 。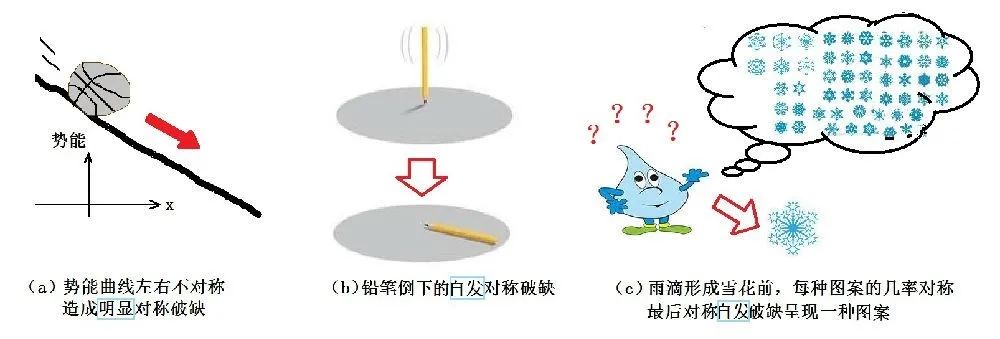

图5：自然界的明显对称破缺和自发对称破缺
图5a中所示是一个在山坡上的石头，山坡造成重力势能的不对称性，使得石头往右边滚动，这是一种明显对称性破缺。在图5b的情况，一支铅笔竖立在桌子上，它所受的力是四面八方都对称的，它朝任何一个方向倒下的几率都相等。但是，铅笔最终只会倒向一个方向，这就破坏了它原有的旋转对称性。这种破坏不是由于物理规律或周围环境的不对称造成的，而是铅笔自身不稳定因素诱发的，所以叫自发对称破缺。图5c的水滴结晶成某个雪花图案的过程也属于自发对称性破缺。
日裔美国物理学家南部阳一郎（Yoichiro Nambu ， 1921-2015）首先将“对称破缺”这一概念从凝聚态物理引进到粒子物理学中[7] 。南部为此和另外两位发现正反物质对称破缺起源的日本物理学家小林诚（Kobayashi Makoto ， 1944-）和益川敏英（Toshihide Maskawa ， 1940-）分享了2008年的诺贝尔物理学奖。
凝聚态物理和粒子物理，初看似乎是风马牛不相干的两个领域，在研究时所涉及的能量级别上也相差几百亿倍，但它们在本质上却有一个共同之处：研究的都是维数巨大的系统，粒子物理基于量子场论，凝聚态物理研究的是连续多粒子体系。量子系统的维数需要趋于无穷大，是自发对称破缺发生的必要条件。与相变相关的“对称破缺”思想，应用于粒子物理，解决了标准模型中的质量问题。
参考文献：
[1].张天蓉科学网博文：《硅火燎原》-21-个性奇特的朗道
http://blog.sciencenet.cn/home.php?mod=space&uid=677221&do=blog&id=724191
[2].于禄，郝柏林。《相变和临界现象》，科学出版社， 1992
[3].L.D. Landau ， On the theory of phase transitions ， 1937
Published in: Zh.Eksp.Teor.Fiz. 7 (1937) 19-32, Phys.Z.Sowjetunion 11 (1937) 26, Ukr.J.Phys. 53 (2008) 25
[4].Anderson, More is different, Science Vol. 177, pp. 393-396（1972）
[5].Kosmann-Schwarzbach, Yvette (2010). The Noether theorems:Invariance and conservation laws in the twentieth century. Sources and Studiesin the History of Mathematics and Physical Sciences. Springer-Verlag.
[6].张天蓉科学网博文：统一路-8-对称和守恒
http://blog.sciencenet.cn/home.php?mod=space&uid=677221&do=blog&id=882465
[7].Nambu, Y.; Jona-Lasinio, G. (April 1961). "DynamicalModel of Elementary Particles Based on an Analogy with Superconductivity.I". Physical Review 122: 345–358.
制版编辑 | 栗子
来源：赛先生

编辑：CHANchan